Задать вопрос Регистрация
Помочь другим

  • Доказать используя математическую индукцию для любого n:

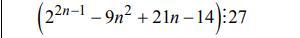
    question img

Ответы 1

  • Уточнение: скорее всего, исходное условие звучало так: Доказать,  используя математическую индукцию, что утверждение верно для любого натурального n.

    Пошаговое объяснение:

    1) n = 1:

    2^1-9*1^2+21*1-14=2-9+21-14=0 \vdots 27

    Верно

    2) Пусть для n = k

    (2^{2k-1}-9k^2+21k-14)\vdots 27

    3) Докажем условие для n = k + 1:

    2^{2(k+1)-1}-9(k+1)^2+21(k+1)-14=2^{2k+1}-9k^2-18k-9+21k+21-14=4*(2^{2k-1}-9k^2+21k-14)+27k^2-3*27k+2*27=((2^{2k-1}-9k^2+21k-14)*4+27*(k^2-3k+2))\vdots 27

    Доказано.

    • Автор:

      bradyo9ki
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years