-
Найти площадь полной поверхности усеченной правильной пирамиды.
ОЧЕНЬ СРОЧНО! Заранее спасибо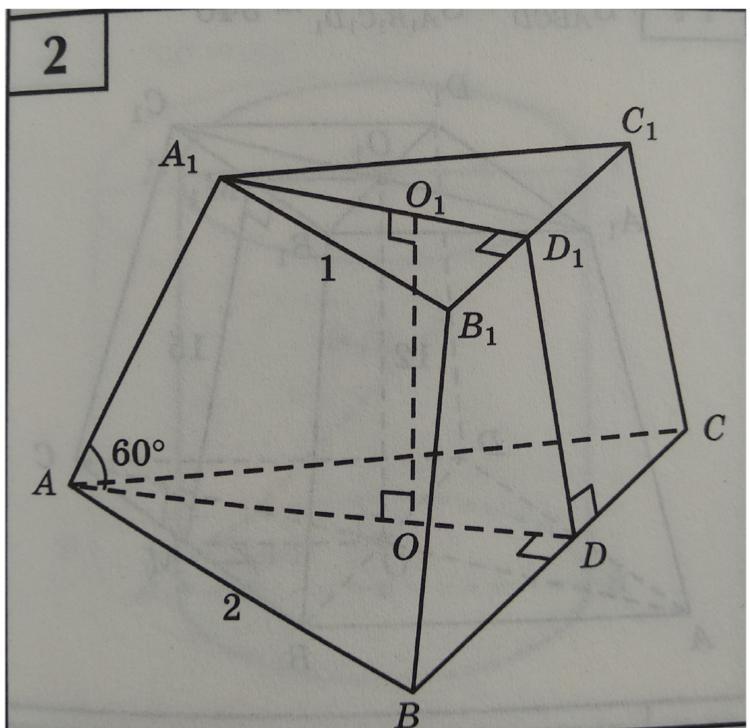
-
Предмет:
Математика -
Автор:
loverep6u - 6 лет назад
-
Ответы 2
-
Ответ: √3+5√0,75
Пошаговое объяснение:
1. Опустим перпендикуляр А1Н из точки А1 на сторону АВ.
АН= (АВ-А1В1)/2=(2-1)/2=0,5
АА1=2АН=1
А1Н=√(АА1²-АН²) =√(1-0,25)=√0,75
2. Площадь АА1В1В
(А1В1+АВ):2×А1Н=(1+2):2×√0,75=1,5√0,75
3. Площадь боковой поверхности пирамиды 3×1,5√0,75=4,5√0,75
4. Высота нижнего основания
АD=√(AB²-AD) =√(4-1)=√3
Площадь нижнего основания
2√3 /2=√3
5. Высота верхнего основания
A1D1=√(A1B1²-A1D1²) =√(1-0,25)=√0,75
Площадь верхнего основания
0,5√0,75
6. Площадь полной поверхности пирамиды
√3+0,5√0,75+4,5√0,75=√3+5√0,75
-
Автор:
jacquelinejnwg - 6 лет назад
-
0
-
-
Площадь нижнего основания равна 2²√3/4=√3
Площадь верхнего основания равна 1²√3/4=√3/4
Площадь боковой поверхности равна произведению полусуммы периметров оснований на апофему. ((3*1+3*2)/2)*ДД₁
Чтобы найти апофему, надо рассмотреть высоты оснований АД и А₁Д₁
Если из вершины А₁ опустить перпендикуляр А₁А₂║О₁О, а из точки Д₁ перпендикуляр Д₁Д₂, легко заметить, что АА₂=ДД₂=(2√3/2/-√3/2)/2=
√3/4
Из ΔА₁А₂А найдем А₁А₂=АА₂tg60°=(√3/4)*√3=3/4
тогда апофема Д₁Д=√(Д₁Д₂²+ДД₂²)=√(9/16+3/16)=√3/2
и площадь боковой поверхности равна (9/2)*(√3/2)=27√3/4
Площадь полной поверхности равна=√3+√3/4+27√3/4=8√3/ед. кв./
-
Автор:
russellm10l - 6 лет назад
-
0
-
-
Добавить свой ответ
-
найти промежутки возрастания функции [tex]y=2+24x-3x^{2} -x^{3}[/tex]
-
Предмет:
Алгебра -
Автор:
pip-squeek - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Подскажите, пожалуйста,
Найдите область значений функции
у= - (х^2+2х)/х^2+2х+3-
Предмет:
Математика -
Автор:
chip26 - 6 лет назад
-
Ответов:
6 -
Смотреть
-
- why do higher spore plants need water for fertilization
-
Нужно сочинение на тему патриотизм
-
Предмет:
Русский язык -
Автор:
jordyn85 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
