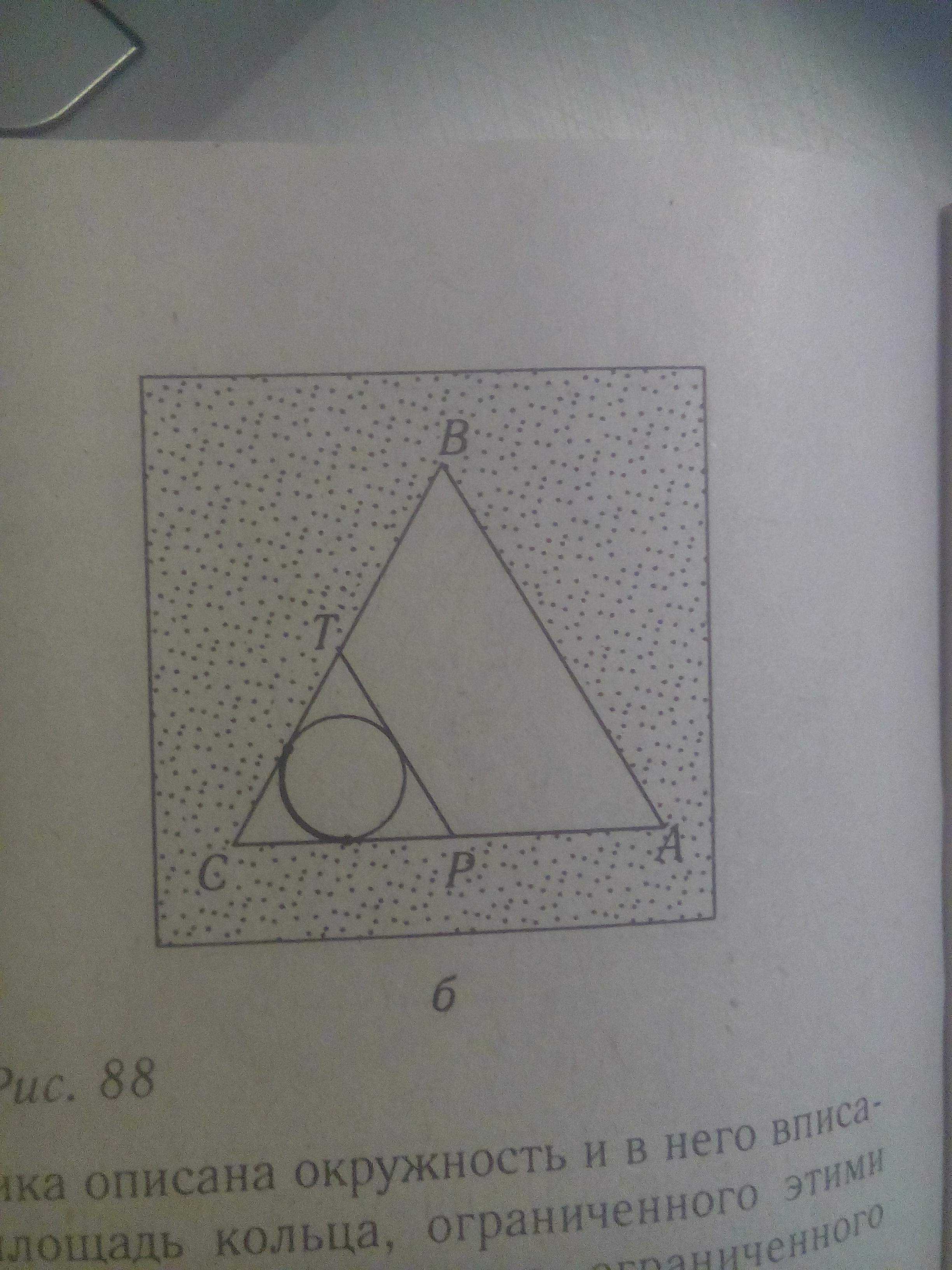
на рисунке изображен равносторонний треугольник ABC. Точки P и T середины сторон AC и CB соответственно. В треугольник CPT вписана окружность. Длина дуги окружностм концами которой являютя точки касания окружности со сторонами BC и AC равна 4П/3 см а ее градусная мера меньше 180. Вычислите длину стороны треугольника ABC

Ответ:

BT=CA=AB=8√3

Пошаговое объяснение:

Для начала обозначим формулы, которыми будем пользоваться:

1) Радиус вписанной окружности в равносторонний треугольник

, где r - радиус, а - сторона треугольника

2)Формула длинны круга через центральный угол

, где l -длинна дуги, B - центральный угол, 180(в градусах)

и так, что мы имеем:

длинна дуги l у нас есть

B < 180 (градусов), тоже по условию задачи

Решение:

ΔАВС равносторонний, поскольку ΔPCT подобный ему он тоже равносторонний

Если провести от точек пересечения окружности и ΔРСТ к центру этой окружности можно заметить, что она делится на 3 сектора (равных между собой)

сумма градусных мер секторов = 360

1 сектор = 120

Теперь всё подставляем в формулу (2) и находим радиус

А сейчас мы собрали все необходимые данные для того, чтобы найти сторону ΔРСТ с помощью формулы (1)

a=2√3 * 2

a=4√3

Поскольку любая сторона ΔАВС в два раза больше любой стороны ΔРСТ (обозначеной как а)

обозначим любую сторону ΔАВС за b

b=2*a

b=2*4√3=8√3