-
Вычислить несобственный интеграл или доказать его расходимость.
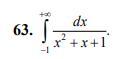
-
Предмет:
Математика -
Автор:
porchelandry - 6 лет назад
-
Ответы 1
-
-
Автор:
johanna - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Что такое обычаи, традиции, обряды, ритуал, мораль, этикет, культура, толерантность, духовная культура. материальная культура
-
Предмет:
Обществознание -
Автор:
honoriomdtn - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Морфологический разбор глагола"спустились"
-
Предмет:
Русский язык -
Автор:
chanel3 - 6 лет назад
-
Ответов:
7 -
Смотреть
-
-
Как решить проблему. Захожу в настройки invidia делаю своё разрешение. Например: 720 на 1080. После чего захожу в игру и оно не отображается. Где только не искал, и в разрешении 4:3, 16:10, 16:9. Помогите исправить это ошибку.
-
Предмет:
Другие предметы -
Автор:
sarahdavila - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
как доказать что в данной пробирке находится нитрат сереьра. запишите уравнения реакции в молекулярном, полном ионном и сокращенном ионном виде
-
Предмет:
Химия -
Автор:
ramiroohvx - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
