Задать вопрос Регистрация
Помочь другим

  • Объясните подробно каждый шаг в решении данного уравнения

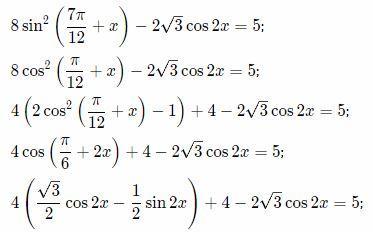
    question img

Ответы 5

  • а по какой формуле удалось свернуть?
  • косинус двойного угла(она написана выше)
  • аа, дошло, мы домножили на два и поэтому в скобках пи/6 + 2х

    • Автор:

      jackson72
    • 5 лет назад
    • 0
  • спасибо, Дружище!

    • Автор:

      alanivyy0
    • 5 лет назад
    • 0

  • Первым действием используют формулы приведения .

    \sin( \frac{7\pi}{12} + x) {}^{2} = \sin( \frac{\pi}{2} + \frac{\pi}{12} + x ) {}^{2} = \cos( \frac{\pi}{12} + x ) {}^{2}

    Дальше приводят к формуле косинуса двойного угла.

    \cos(2 \alpha ) = 2 \cos( \alpha ) {}^{2} - 1

    Для этого добавляют у вычитают 4 и сразу же выносят ее за скобку.

    Потом сворачивают по формуле и используют формулу

    \cos( \alpha + \beta ) = \cos( \alpha ) \cos( \beta ) - \sin( \alpha ) \sin( \beta )

    Теперь раскроем скобки и досчитаем уравнение

    2 \sqrt{3} \cos(2x) - 2 \sin(2x) + 4 - 2 \sqrt{3} \cos(2x) = 5 \\ - 2 \sin(2x) + 4 = 5 \\ - 2 \sin(2x) = 1 \\ \sin(2x) = - \frac{1}{2} \\ 2x = - \frac{\pi}{6} + 2\pi k \\ 2x = - \frac{5\pi}{6} + 2\pi k \\ x = - \frac{\pi}{12} + \pi k \\ x = - \frac{5\pi}{12} + \pi k

    Везде нужно дописать

    k \in \mathbb Z

    • Автор:

      sergio41
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years