Задать вопрос Регистрация
Помочь другим

  • Помогите решит дифференциальное уравнение. номер 3979

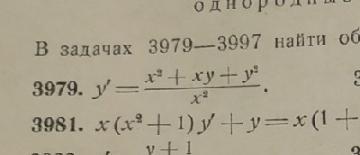
    question img

Ответы 1

  • Пошаговое объяснение:

    Данное дифференциальное уравнение является однородным.

    Пусть y = ux, тогда y' = u'x + u.

    u'x+u=\dfrac{x^2+ux^2+u^2x^2}{x^2}\\ \\ u'x+u=1+u+u^2\\ \\ u'x=1+u^2

    Получили уравнение с разделяющимися переменными

    \dfrac{du}{dx}=\dfrac{1+u^2}{x}~~~\Longleftrightarrow~~~ \displaystyle \int\dfrac{du}{1+u^2}=\int\dfrac{dx}{x}\\ \\ \\ {m arctg}\, u=\ln |x|+C\\ u={m tg}\, \left(\ln |x|+Cight)~~~~\Longrightarrow~~~~ \boxed{y=x{m tg}\left(\ln |x|+Cight)}

    • Автор:

      eddypark
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years