-
Исследуйте ряд на сходимость
Задание 5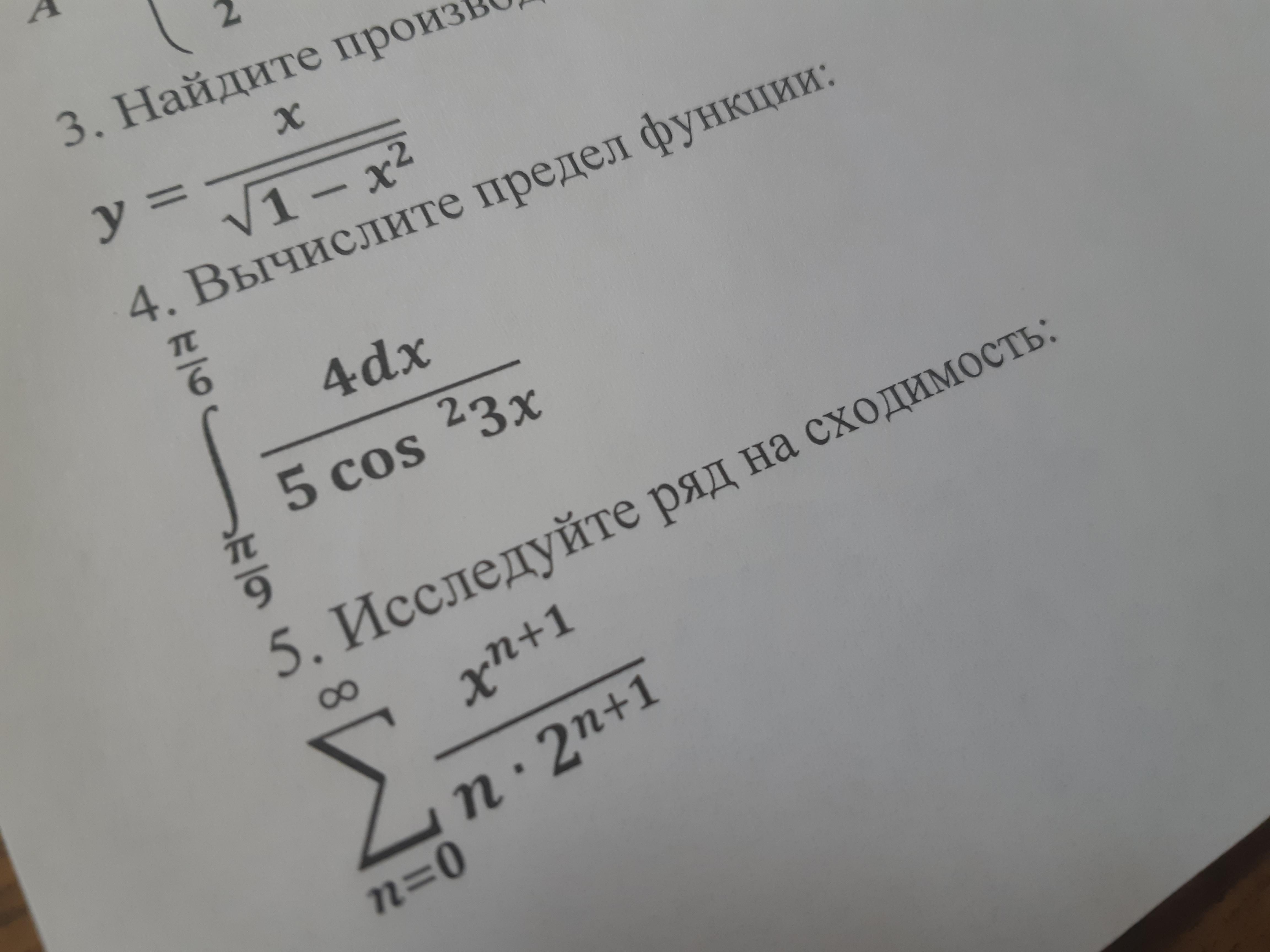
-
Предмет:
Математика -
Автор:
natashaxix2 - 6 лет назад
-
Ответы 1
-
Ответ:
Пошаговое объяснение:
Сделаем замену k=n+1;
∑
R=
область сходимости = (-2;2)
ряд расходится = (-∞;-2)∪[2;+∞);
x=2 ∑
ряд расходится
x=-2 ∑
ряд условно сходится
-
Автор:
moonshineprince - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Нужно сделать по немецкому приглашения и сколько там будет гостей сколько количество стаканов ну и т.д
-
Предмет:
Немецкий язык -
Автор:
willow23 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
- Положение Великобритании относительно условных линий на карте! Помогите пожалуйста, нигде не могу найти!
-
Разложите на множители: 16m6(cтепень)n2(степень)-81х2(степень)
-
Предмет:
Математика -
Автор:
dharma - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
ОСУЩЕСТВИТЬ ПРЕОБРАЗОВАНИЯ!100 БАЛЛОВ!!!!!
(C6H10O5)n -->C6H1206-->CH3CH2OH-->CH2=CH2-->CH2OH-CH2OH
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
↓
⠀⠀⠀⠀⠀(CH2OH-(CHOH)4-COOH)
How much to ban the user?
1 hour
1 day
100 years
