-
Тригонометрическое уравнение, какие формулы и как применять при его решении?Не могу понять, по каким формулам оно решается.
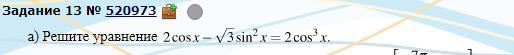
-
Предмет:
Математика -
Автор:
costa - 6 лет назад
-
Ответы 3
-
Спасибо огромное!
-
Автор:
spike - 6 лет назад
-
0
-
-
Ответ:
x=-π/6+2πm x=π/6+2πm m∈Z
x=πn n∈Z
Пошаговое объяснение:
2cosx-√3sin²x=2cos³x используем sin²x+cos²x=1 sin²x=1-cos²x
2cosx-√3(1-cos²x)-2cos³x=0
2cosx-√3+√3cos²x-2cos³x=0
(2cosx-2cos³x)-(√3-√3cos²x)=0
2cosx(1-cos²x)-√3(1-cos²x)=0
(1-cos²x)(2cosx-√3)=0
1-cos²x=0 или 2cosx-√3=0
1-cos²x=0 используем cos2x=cos²x-sin²x cos2x=2cos²x-1 cos²x=(cos2x+1)/2
1-(cos2x+1)/2=0
(2-cos2x-1)/2=0
1-cos2x=0
cos2x=1 2x=2πn x=πn, n∈Z
2cosx-√3=0
2cosx=√3
cosx=√3/2 x=-arccos√3/2+2πm x=arccoa√3/2+2πm arccos√3/2=π/6
x=-π/6+2πm x=π/6+2πm m∈Z
-
Автор:
tacoodud - 6 лет назад
-
0
-
-
переносим 2cos^3x влево
2cosx-2cos^3x-√3sin^2x=0
2cosx(1-cos^2)-√3sin^2=0
Из основного тригонометрического тождества следует, что:
cos^2x+sin^2x=1, значит sin^2x=1-cos^2x
Заменяем скобку на sin^2x, получается:
2cosx*sin^2x-√3sin^2=0
sin^2x(2cosx-√3)=0
Каждый множитель приравниваем к нулю
2cosx=√3
cosx=√3/2
x= П/6+2Пn; n принадлежит z
x= -П/6+2Пn; n принадлежит z
sin^2x=0
sinx=0
x=Пn; n принадлежит z
Ответ: x= П/6+2Пn ; x= -П/6+2Пn ; Пn
-
Автор:
isiscpnu - 6 лет назад
-
0
-
-
Добавить свой ответ
-
тибитьитьитбитбитбитбитбибитбит
-
Предмет:
История -
Автор:
yadielmercer - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В парке посадили 17 саженцев березы это 5 раз меньше чем дубов, А лип на 9 кустов больше чем дубов .На сколько саженцов лип чем саженцов березы посадили в парке
-
Предмет:
Математика -
Автор:
denver - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Скоротіть дріб 10x^3y/15y^2x
-
Предмет:
Математика -
Автор:
trippiq1c - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Рассказать самое главное о абиотических факторах среды
