-
В основании пирамиды SABCD лежит квадрат, и высота пирамиды SB. Боковое ребро AS образует с основанием пирамиды угол 30 градусов.
а) Вычислите значение угла SAD. Обоснуйте.
б) Докажите, что площадь грани ASB равна 1/6 от площади боковой поверхности пирамиды.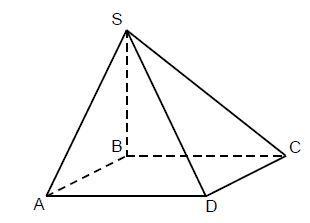
-
Предмет:
Математика -
Автор:
alex84 - 6 лет назад
-
Ответы 1
-
а) Прямая AD перпендикулярна двум прямым АВ и SВ, лежащим в плоскости АВS, поэтому по теореме о трех перпендикулярах она перпендикулярна и любой прямой, принадлежащей этой плоскости, значит перпендикулярна и прямой SA.
Ответ: угол SAD равен 90 градусов.
б) Примем сторону основания за 1.
Если боковое ребро AS образует с основанием пирамиды угол 30 градусов, то высота пирамиды SВ равна 1*tg 30 = 1/√3.
Площади граней SAВ и SВС равны по (1/2)*1*(1/√3) = 1/(2√3).
Боковое ребро SA равно SС и равно √(1² + (1/√3)²) = √(4/3) = 2/√3.
Площади граней SAD и SСD равны по (1/2)*1*(2/√3) = 1/√3.
Площадь боковой поверхности равна:
Sбoк = 2*(1/(2√3)) + 2*(1/(√3)) = 3/√3.
Отношение площади грани SAВ к Sбoк равно:
SAВ/Sбoк = (1/(2√3) )/(3/√3) = 1/6.
-
Автор:
tavianij3j - 6 лет назад
-
0
-
-
Добавить свой ответ
-
при сливании растворов каких либо веществ происходит реакция описываемая сокращенным ионным уравнением Н+ +ОН- Н2О:
1. гидроксид бария и серная кислота
2. гидроксид магния и азотная кислота
3. гидроксид калия и бромоводорода
4. гидроксид меди и азотная кислота
5. гидроксид натрия и уксусная кислота
6. гидрокарбонат натрия и гидроксид натрия -
пожалуйста помогите мне пожалуйста помогите мне
и задание к нему
2)Answer each question in1 or 2 sentences
1.what is janes' s father' s problem?___________________________________________________________________________________________________________________________
2. Why didn' t the white flag help jane 's father?___________________________________________________________________________________________________________________________
3. Find 3 verbs in Present Simple and write.______________ -
Предмет:
Английский язык -
Автор:
chewbacca - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Напишите уравнения реакций,с помощью которых можно продемонстрировать свойства оснований на примере гидроксида калия и гидроксида меди. Напишите сокращенные и полные ионные уравнения реакций
-
Предмет:
Химия -
Автор:
chiliburke - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- срочно!!!!!скажите пожалуйста где в музыке используют рациональные числа
