-
При каких a уравнение будет иметь ровно два решения
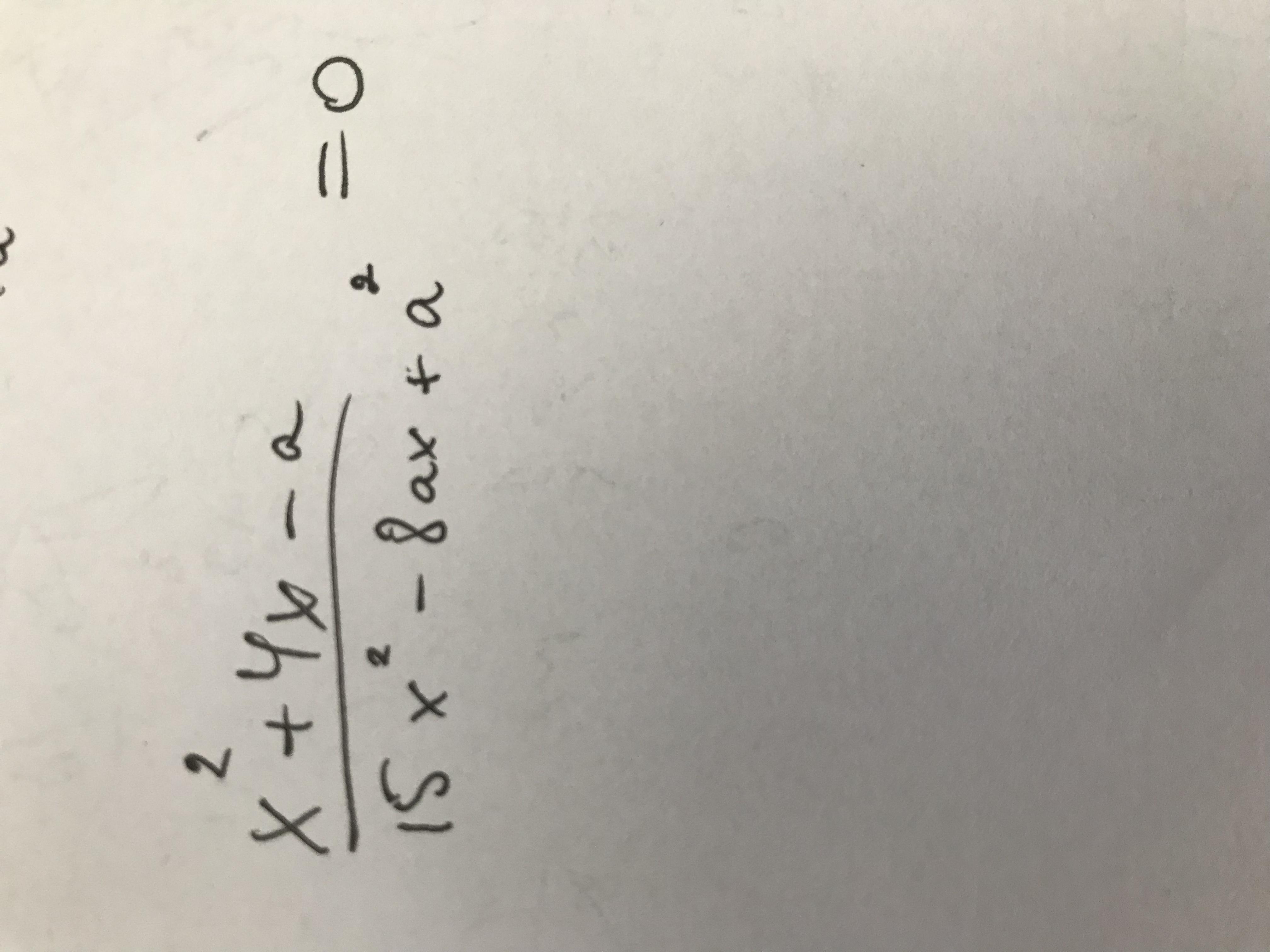
-
Предмет:
Математика -
Автор:
kierstenl5xs - 6 лет назад
-
Ответы 1
-
Ответ:
Пошаговое объяснение:
В числителе стоит квадратный трёхчлен, у него может быть не более 2 корней. Значит, чтобы у уравнения было ровно 2 различных корня, числитель должен иметь 2 корня, и ни один из корней числителя не должен быть корнем знаменателя.
У числителя два неравных корня, если дискриминант больше нуля:
Ищем корни знаменателя:
Итак, нужно, чтобы ни x = a/3, ни x = a/5 не были корнями числителя:
Выкалываем найденные точки из решения неравенства a > -4 и получаем ответ.
-
Автор:
waynephw0 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
ПОМОГИТЕ !С РЕШЕНИЕМ
1. Упростить выражение; (2x-3)²-4x²-5
2. Упростить выражение; √12+√27
_______
√3
3. Найти разность дробей; 3 x+15
___ - __
x-3 x²-9
4.Решить неравенство дробей; 5x+8≤4x-12
5. Решить квадратные уравнения; а) x²=9 б) x²-5x=0 в) 2x²-3x-2=0
Эти чёрты это дроби если что _______-
Предмет:
Математика -
Автор:
adancontreras - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Составить словарный диктант на правописание сущ., прилаг, числит. и местоим. (20-25 слов).
-
Предмет:
Русский язык -
Автор:
bradyburns - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Срочно!
Дано: треугольник АВС-равносторонний. Найти АВ
Подробно пожалуйста
Рис.776-
Предмет:
Математика -
Автор:
alessandrou6xd - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
пожалуйста помогите !!!! математике у меня экзамен .
-
Предмет:
Математика -
Автор:
miasyha3k - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
