-
Решите неравенство, с объяснением . Даю 40 баллов.
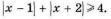
-
Предмет:
Математика -
Автор:
marvinramsey - 6 лет назад
-
Ответы 3
-
А зачем в Вашем примере модель?) Я же не отправляю Вас в нарушители. Зачем же Вы меня за знак объединения?(
-
Автор:
lillymarshall - 6 лет назад
-
0
-
-
|x - 1| + |x + 2| ≥ 4
вспомним по-простому что такое модель
|x| = x x≥0
и -x x<0
ну и по простому будет "открывать" модули в зависимости от значений х
|x+2| = 0 |x-1| = 0 точки перехода -2 и 1
Таблицф по вертикали значения переменной, по горизонтали значение модулей
|x + 2| |x-1|
x<-2 -x-2 1-x (1)
1>x>=-2 x+2 1-x (2)
x>=1 x+2 x-1 (3)
1. x<=-2
-x-2 + 1-x ≥ 4
-2x ≥ 5
2x ≤ - 5
x≤ -2.5
x∈(-∞ -2.5]
2. -2≤ x < 1
x+2 + 1-x ≥ 4
3 ≥ 4
решений при таких икс нет x∈∅
3. x≥ 1
x+2 + x-1 ≥ 4
2x ≥ 3
x ≥ 3/2
x≥ 1.5
x∈[1.5 +∞)
объединяем все три ответа и получаем
Ответ x∈(-∞ - 2.5] U [1.5 +∞)
-
Автор:
malachi15 - 6 лет назад
-
0
-
-
Приравниваем нулю подмодульные выражения, получаем точки х=1 и х=-2, ими разбиваем числовую прямую на три интервала и на каждом определяем решение, с учетом интервала, снимая модули.
1. х∈(-∞;-2]; 1-x-x-2≥4; -2х≥5, х≤-2.5
2. х∈(-2;1]; 1-х+х+2≥4 неверное неравенство, на этом интервале нет решений.
3. х∈(1;+∞); х-1+х+2≥4;2х≥3; х≥1.5;
объединим два решения и получим ответ
х∈(-∞;-2.5]∪ [1.5;+∞)
-
Автор:
toribioq61x - 6 лет назад
-
0
-
-
Добавить свой ответ
-
СРОЧНО!!!!!!!!!!!!!!!!!!
ДАЮ 40 БАЛОВ!!!!!!!!!!!!!!!!!
Участок ДНК кодирующий структуру какого-нибудь белка ,называют: 1)ген 2)ядро 3)митоз -
Найти корень уравнения:
(7-x)^2=(-18-x)^2 -
Решить неравенство. 1.Log²(5-2x)<1 2.решить уравнение sin2x=3cos x
-
Предмет:
Алгебра -
Автор:
savannah37 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите составить предложения с глагола ми :can, could, be able to, was able to
-
Предмет:
Английский язык -
Автор:
adalyno6gt - 6 лет назад
-
Ответов:
1 -
Смотреть
-
