Задать вопрос Регистрация
Помочь другим

  • Вычислить пределы функций, используя I, II замечательные пределы и эквивалентность БМФ.

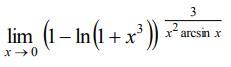
    question img

Ответы 1

  • При \sf x ightarrow 0  \sf \arcsin x \sim \sin x \sim x;

    Таким образом, можно переписать предел:

    \sf \lim \limits_{xightarrow 0}(1-\ln(1+x^{3}))^{\frac{3}{x^{3}}; Удобно сделать замену: \sf x^{3}:=\frac{1}{t}; Предел получится таким:

    \sf\lim \limits_{t\to \infty}(1-\ln(\frac{t+1}{t}))^{3t}=\lim\limits_{t\to\infty}(1-\ln(\frac{1}{t})-\ln(t+1))^{3t}; Воспользуемся следующим фактом: \sf\log_{a}x \sim \frac{x}{\ln a},\; \textbf{if}\;\; x\to 0 При этом \sf\ln(1+x) \sim x ; Тогда: \sf\lim\limits_{t\to\infty}(1-\ln(1+\frac{1}{t}))^{3t}=\lim\limits_{t\to\infty}(1-\frac{1}{t})^{3t}=\lim\limits_{t\to\infty}(\frac{t-1}{t})^{3t}=\lim\limits_{t\to\infty}(\frac{t}{t+1})^{3t}=\lim\limits_{t\to\infty}(1+\frac{1}{t})^{-3t}; Последний предел очевиден: \sf\lim\limits_{t\to\infty}((1+\frac{1}{t})^{t})^{-3}=e^{-3}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years