-
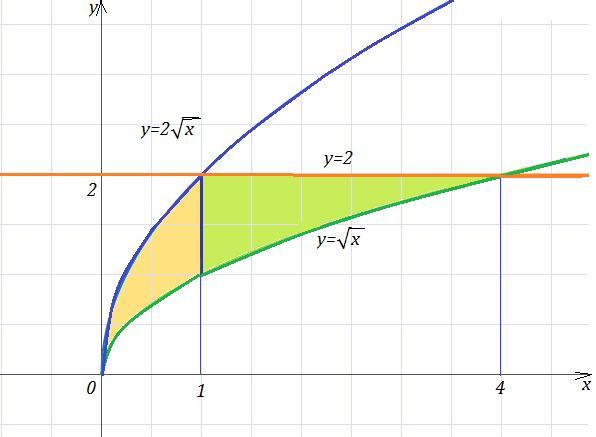
Вычислить площадь фигуры, ограниченной линиями с помощью определённого интеграла, сделать иллюстрацию y=√x, y=2√x, y=2.
-
Предмет:
Математика -
Автор:
heisenberg - 6 лет назад
-
Ответы 2
Еще вопросы
-
Когда перевезли четверть груза, то осталось ещё 24 тонны. Какова масса груз?
-
Предмет:
Математика -
Автор:
cassie - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Когда перевезли четверть груза, то осталось ещё 24 тонны. Какова масса груз?
-
Предмет:
Математика -
Автор:
sidney - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Для функции f(x)=x+2x^5 найдите первообразную F(x)
-
Спростить вираз
Sin 5a cos 3a -cos 5a sin 3a-
Предмет:
Математика -
Автор:
norahclarke - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years