-
найти производную сложной функции
2^(x-2*x^2-1)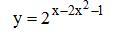
-
Предмет:
Математика -
Автор:
myliegould - 6 лет назад
-
Ответы 3
-
спасибо!
-
Автор:
bibblessullivan - 6 лет назад
-
0
-
-
-
Автор:
maximilianncgc - 6 лет назад
-
0
-
-
Ответ:
Пошаговое объяснение:

-
Автор:
virgiliomejia - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Вычислить (a-альфа)
4sin(3п/2-а)*cos(п/2+а)*cos(п+2a)-
Предмет:
Алгебра -
Автор:
juliusnunez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В ящике лежат 58 овощей, масса каждого из которых выражается целым числом граммов. В ящике есть хотя бы два овоща различной массы, а средняя масса всех овощей равна 1000 г. Средняя масса овощей, масса каждого из которых меньше 1000 г, равна 976 г. Средняя масса овощей, масса каждого из которых больше 1000 г, равна 1036 г.
а) Могло ли овощей меньше и больше 1000г быть поровну?
б) Могло ли в ящике оказаться 12 овощей массой ровно 1000г?
в) Какую наименьшую массу может иметь овощ в этом ящике?-
Предмет:
Математика -
Автор:
clayukq3 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Обчислити площу фігури, обмеженої лініями
У=3x-x^2 y=x - 7(3x-1)+5(x-3)=0 пожалуйста
How much to ban the user?
1 hour
1 day
100 years
