-
Срочно! 95 баллов. Помогите решить интеграл с заменами переменных обязательно!
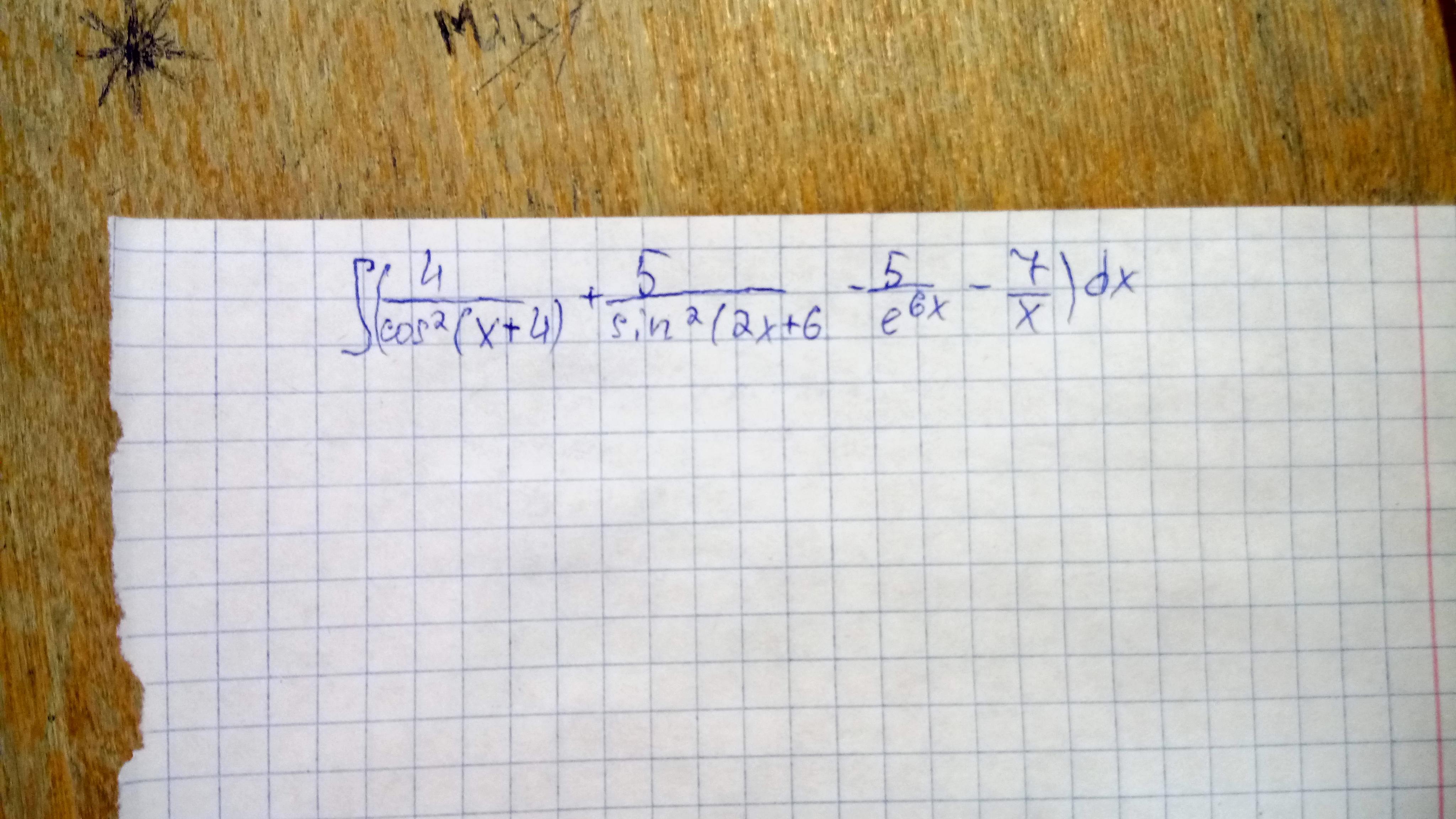
-
Предмет:
Математика -
Автор:
cristian9ucf - 6 лет назад
-
Ответы 2
-
находим интегралы по членно

-
Автор:
wally - 6 лет назад
-
0
-
-
∫(4/(cos²(x+4))+5/(sin²(2x+6))-5/e⁶ˣ-7/x)dx=
4tg(x+4)-(5ctg(2x+6))/2)-5(e⁻⁶ˣ/(-6)) - 7*㏑IxI+c=
4tg(x+4) - 2.5ctg(2x+6)) + 5/6e⁶ˣ - 7*㏑IxI+c
Проверка (4tg(x+4)-2.5ctg(2x+6)) + 5/(6e⁶ˣ) -7*㏑IxI+c)'=
(4/cos²(x+4))+5/sin²(2x+6)) -6*(5/6)*e⁻⁶ˣ/ -7/x=
4/(cos²(x+4))+5/(sin²(2x+6))-5/e⁶ˣ-7/x)
Ответ 4tg(x+4)-2.5ctg(2x+6))+5/6e⁶ˣ -7*㏑IxI+c
Использовал табличные интегралы ∫(1/(cos²(аx+в))=(tg(аx+в))/a)+с;
∫(1/(sin²(аx+в))=-(ctg(аx+в))/a)+c
∫dx/x=㏑IxI+c
∫eᵃˣ=(eᵃˣ/а)+с

-
Автор:
nolan58 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Mard maydonda sinalar maqolining mazmunini tushuntirib bering
-
Предмет:
Оʻzbek tili -
Автор:
saul - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
У Лены 8 монет по 5 рублей . Сколько рублей у Лены .
Нужно условие-
Предмет:
Математика -
Автор:
bobogibson - 6 лет назад
-
Ответов:
3 -
Смотреть
-
- площі основ зрізаної чотирикутної піраміди 27 і 12 см^2, а висота 5 см. обчислити висоту, яка відповідає повній піраміді
-
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 3√2. Найдите объём параллелепипеда.
-
Предмет:
Геометрия -
Автор:
kennedirivas - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
