-
75 БАЛЛОВ | Математика 10-11 класс
ПОДРОБНОЕ РЕШЕНИЕ №1-3, желательно приложить фото решения!!!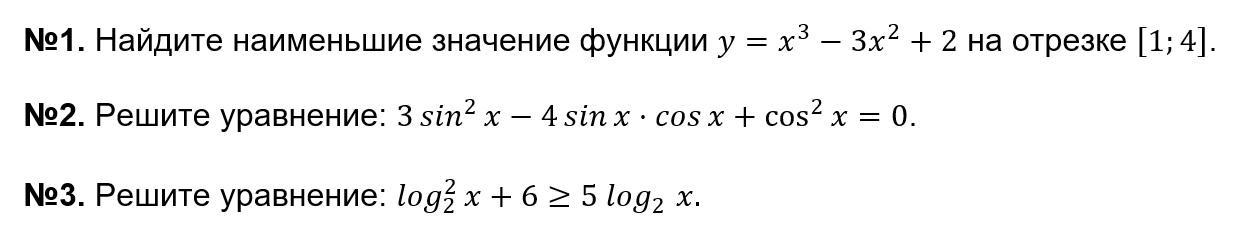
-
Предмет:
Математика -
Автор:
Ángelramirez - 6 лет назад
-
Ответы 7
-
Пользуйтесь.)
-
Автор:
coco63 - 6 лет назад
-
0
-
-
а здесь какая ошибка?)
-
Автор:
loreleioneal - 6 лет назад
-
0
-
-
В 3 неравенство. Найдены корни, и не вспомнилось, что это неравенство. Мне написали, что исправить. А как?
-
Автор:
bearwatson - 6 лет назад
-
0
-
-
Модератор!!! Отправьте мне на исправление.
-
Автор:
kylan - 6 лет назад
-
0
-
-
Автору вопроса. В 3) там поставить знаки log(2)x<=2 и loq(2)x>=3, отсюда х<=4, х>=8. С учётом ОДЗ ответ: (0;4]U[8;+беск)
-
Автор:
tango - 6 лет назад
-
0
-
-
Відповідь:
Покрокове пояснення:

-
Автор:
patriciomarquez - 6 лет назад
-
0
-
-
1. найдем критические точки, приравняв к нулю производную. 3х²-6х=0, 3х(х-2)=0, откуда х=0 ∉[1;4]; х=2∈[1;∈4]; Найдем у(1)=1-3+2=0; у(2)=8-3*4+2=-2;- наименьшее значение функции; у(4)=4³-3*4²+2=66-48=18.
2. 3sin²x-4sinxcosx+cos²x=0, однородное уравнение, разделим его на cos²x≠0, т.к. одновременно косинус и синус не могут быть нулями. Получим 3tg²x-4tgx+1=0; tgx=у, 3у²-4у+1=0, у=(4±√(16-12))/6; у₁=(4+2)/6=1;
у₂=1/3, если tgx=1, то х= π/4+πn; n∈Z; если tgx=1/3, то х= аrctg1/3+πn; n∈Z
3. ОДЗ х∈(0;+∞) пусть ㏒₂х=у, у²-5у+6=0, ПО Виета, у=3, у=2, тогда (у-2)*(у-3)≥0 решим методом интервалов.
__2_______3__________
+ - +, решением неравенства будет
(-∞;2]∪[3;+∞)
㏒₂х≤2, основание логарифма 2 больше 1, поэтому х≤4;
㏒₂х≥3; по той же причине знак неравенства не меняется х≥8 . С учетом ОДЗ получим ответ х∈(0;4]∪[8;+∞)
Ответ х∈(0;4]∪[8;+∞)

-
Автор:
almudenajeuz - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Дан куб АВСDA1B1C1D1 . Найдите градусную меру угла, гранями которого являются плоскости (ABC) и (ABC1).
-
Предмет:
Математика -
Автор:
joliehzeo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Христианская средневековая цивилизация в европе кратко
-
Изотоническим раствором для теплокровных животных и человека
является 0,9%-ный раствор хлористого натрия. Определить его осмотическое
давление при температуре 37оС, считая, хлористый натрий полностью
диссоциированным. Молярная масса хлористого натрия 58 г/моль - положительные и отрицательные особенности политико-географического положения Франции
