Задать вопрос Регистрация
Помочь другим

  • f(xy) = y/ x^2-y^2

    помогите решить, буду благодарен.
    нужно найти частные производные ​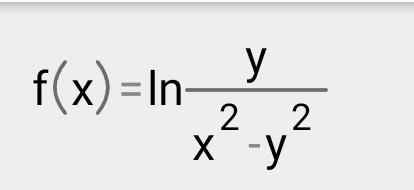

    question img

Ответы 1

  • f(x,y)=\ln\left(\frac{y}{x^2-y^2} ight)\\\frac{\partial f}{\partial x}=\frac{x^2-y^2}{y}*\left(-\frac{y*2x}{(x^2-y^2)^2}ight)=-\frac{2x}{x^2+y^2}

    Чтобы было легче взять производную по у воспользуемся свойствами логарифма

    f(x,y)=\ln(y)-\ln(x^2-y^2)\\\frac{\partial f}{\partial y}=\frac{1}{y}-\frac{-2y}{x^2-y^2}=\frac{1}{y}+\frac{2y}{x^2-y^2}

    • Автор:

      oliveuetc
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years