Пожалуйста, помогите с решением дифференциального уравнения и задачи Коши.

Пожалуйста, помогите с решением дифференциального уравнения и задачи Коши.
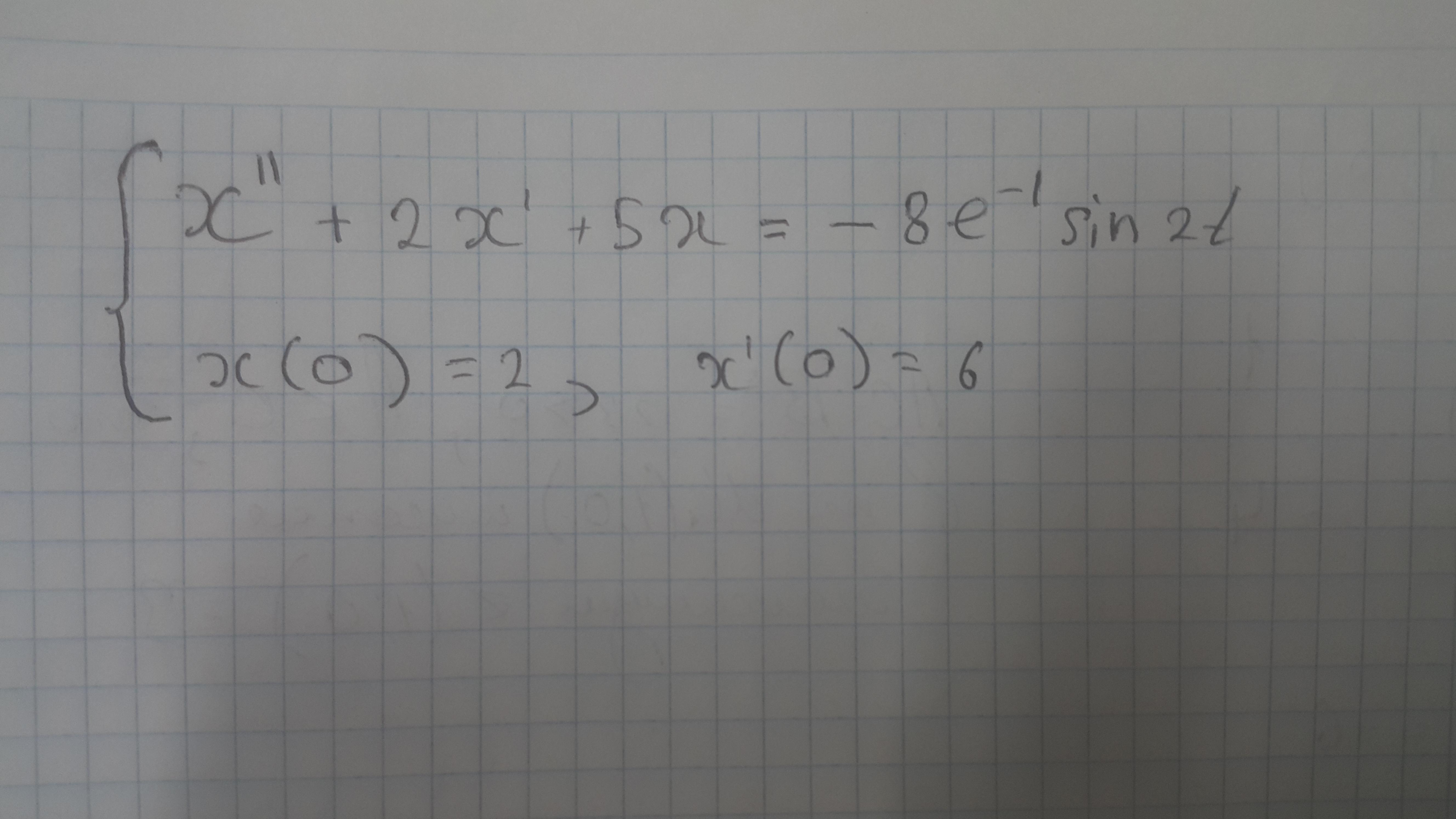
- Предмет:
  Математика
- Автор:
  paris
- 5 лет назад

Ответы 1

Найдем сначала общее решение соответствующего однородного дифференциального уравнения:
$x''+2x'+5x=0$
Используя замену $x'=e^{kt}$ , получим характеристическое уравнение
$k^2+2k+5=0$
$k=-1\pm 2i$
Общее решение однородного дифференциального уравнения:
$x^*=C_1e^{-t}\cos 2t+C_2e^{-t}\sin 2t$
Рассмотрим функцию: $f(t)=-8e^{-1}\sin 2t$ . Здесь $P_n(t)=-8e^{-1}$ откуда $n=0;$ и $\alpha=0;~\beta=2;~~~Q_n(t)=0$ . Сравнивая α, β с корнями характеристического уравнения, частное решение будем искать в виде:
$x^{**}=A\sin 2t+B\cos 2t\\ x'=(A\sin2t+B\cos 2t)'=2A\cos 2t-2B\sin 2t\\ x''=(2A\cos 2t-2B\sin 2t)'=-4A\sin2t-4B\cos 2t$
Подставляем в исходное дифференциальное уравнение:
$-4A\sin2t-4B\cos 2t+4A\cos2t-4B\sin2t+5A\sin2t+5B\cos2t=-8e^{-1}\sin2t$
$A\sin2t+B\cos2t+4A\cos2t-4B\sin2t=-8e^{-1}\sin2t\\ \\ \sin2t(A-4B)+\cos 2t(B+4A)=-8e^{-1}\sin 2t$
Приравниваем коэффициенты при cos2x и sin2x, получаем систему:
$\displaystyle \left \{ {{A-4B=-8e^{-1}} \atop {B+4A=0}} ight.~~~\Rightarrow~~~\left \{ {{A+16A=-8e^{-1}} \atop {B=-4A}} ight.~~~\Rightarrow~~~\left \{ {{A=-\frac{8}{17}e^{-1}} \atop {B=\frac{32}{17}e^{-1}}} ight.$
Общее решение линейного неоднородного дифференциального уравнения:
$x=x^*+x^{**}=C_1e^{-t}\cos 2t+C_2e^{-t}\sin 2t-\frac{8}{17}e^{-1}\sin 2t+\frac{32}{17}e^{-1}\cos 2t$
Осталось решить задачу Коши, подставляя начальные условия
$x'=(C_1e^{-t}\cos 2t+C_2e^{-t}\sin 2t-\frac{8}{17}e^{-1}\sin 2t+\frac{32}{17}e^{-1}\cos 2t)'=\\ =-C_1e^{-t}\cos2t-2C_1e^{-t}\sin2t-C_2e^{-t}\sin2t+2C_2e^{-t}\cos 2t-\\ -\frac{16}{17}e^{-1}\cos2t-\frac{64}{17}e^{-1}\sin2t\\ \\ x'(0)=2;~~~2=-C_1+2C_2-\frac{16}{17}e^{-1}\\ x(0)=6;~~~~6=C_1+\frac{32}{17}e^{-1}$
$\displaystyle \left \{ {{2=-C_1+2C_2-\frac{16}{17}e^{-1}} \atop {6=C_1+\frac{32}{17}e^{-1}}} ight.~~~~\Rightarrow~~~~\left \{ {{C_2=4+\frac{8}{17}e^{-1}} \atop {C_1=6-\frac{32}{17}e^{-1}}} ight.$
Частное решение задачки Коши:
$x=(6-\frac{32}{17}e^{-1})e^{-t}\cos 2t+(4+\frac{8}{17}e^{-1})e^{-t}\sin 2t-\frac{8}{17}e^{-1}\sin 2t+\frac{32}{17}e^{-1}\cos 2t$
- Автор:
  grumpy
- 5 лет назад
- 0
Добавить свой ответ