-
Пожалуйста, решите с пояснениями (для человека, весьма слабо разбирающегося в логарифмах)
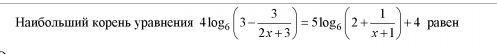
-
Предмет:
Математика -
Автор:
yairfry - 6 лет назад
-
Ответы 5
-
Большое спасибо!
-
Автор:
deborahmays - 6 лет назад
-
0
-
-
Добрый день! Вчера не было возможности разобраться в этом, но сегодня она появилась, а у меня появился вопрос. Не могу понять, откуда взялась 6 в степени 4, если изначально была просто 4?
-
Автор:
haroldxiin - 6 лет назад
-
0
-
-
4=4*1=4*log(6)6=log(6)6^4
-
Автор:
atanasio - 6 лет назад
-
0
-
-
О, теперь дошло, огромное спасибо)
-
Автор:
dash81 - 6 лет назад
-
0
-
-
ОДЗ:
Метод интервалов:
__+__ (-3/2) ___ (-1) __+___
x∈(-∞;-3/2) U (-1;+∞)
Свойства логарифма.
Логарифм степени
n·log_(6)b=log_(6)bⁿ
b>0
Логарифм произведения
log_(6) a + log_(6)b=log_(6)a·b
a>0; b>0
Уравнение принимает вид:
log₆(6(x+1)/(2x+3))⁴=log₆((2x+3)/(x+1))⁵·6⁴
Логарифмы равны, значит и выражения под логарифмами равны.
(6(x+1)/(2x+3))⁴=((2x+3)/(x+1))⁵·6⁴
Сокращаем на 6⁴
(х+1)⁴/(2х+3)⁴=(2х+3)⁵/(х+1)⁵
((x+1)/(2x+3))⁹=1
(x+1)/(2x+3)=1
x+1=2x+3
x=-2∈(-∞;-3/2) U (-1;+∞)
О т в е т. -2
-
Автор:
porter98 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
диагональ осевого сечения цилиндра равна 10 см, а высота равна 8 см. Найдите радиус цилиндра
-
Предмет:
Математика -
Автор:
azaria - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Решите уравнение
7log√2(5-x)=49log4(35-7x)-
Предмет:
Математика -
Автор:
trey - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
стороны основания прямоугольного параллелепипеда равны 2 см и 3 см, а диагональ 7 см. Найдите боковую сторону параллелепипеда
-
Предмет:
Математика -
Автор:
stormy - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Установите соответствие между предложениями и их характеристикой:
А: Когда мы приехали в лагерь, там вовсю уже кипела работа: мальчики таскали дрова, ставили палатки, распаковывали груз.
Б: Кошка скосила глаза и увидела: неподалёку от буфета маленький мышонок забегал по полю, настороженно поглядывая в ее сторону.
В: Ничто не может защитить от горестей и бед: ни знатный род, ни красота, ни сила, ни богатство.
Г: Климат здесь был мягкий, и дружно росли в этой местности деревца всех пород: ель, сосна, берёза и осина.
1. простое осложнённое предложение
2. сложносочинённое предложение
3. сложноподчинённое
4. бессоюзное сложное предложение
5. сложное предложение с разными видами связи-
Предмет:
Русский язык -
Автор:
keesha - 6 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
