-
3ln(x)*sin^2(y)=y' пожалуйста,горю у меня решено так
не подходит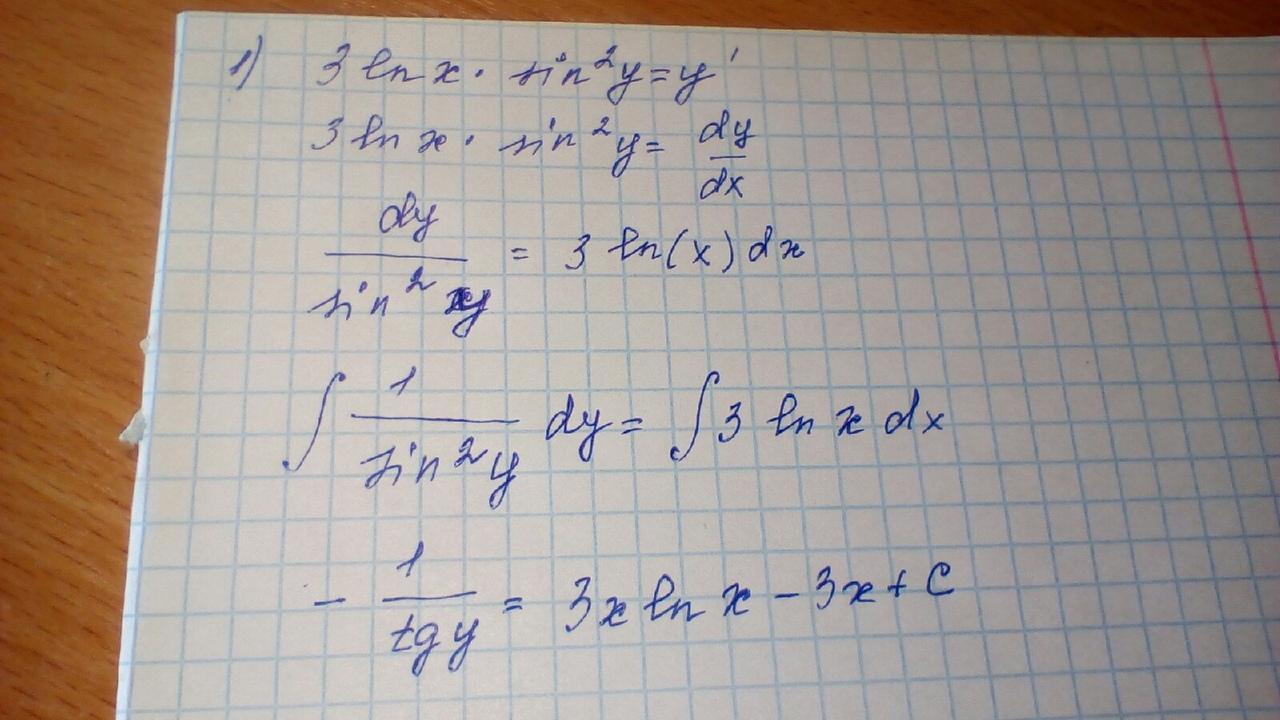
-
Предмет:
Математика -
Автор:
maren - 6 лет назад
-
Ответы 3
-
Решение исправил
-
Автор:
alfredo - 6 лет назад
-
0
-
-
Это уравнение с разделяющимися переменными.
Посчитаем интеграл правой части уравнения по частям
Мы получим:
-
Автор:
gabriellaf60e - 6 лет назад
-
0
-
-
3㏑х*sin²у=y' - это уравнение с разделяющимися переменными. Разделим переменные. 3㏑х*sin²у=dy/dx⇒ 3㏑хdx=dy/sin²у;
∫3㏑хdx=∫dy/sin²у
Возьмем интеграл от левой части. Будем интегрировать по частям по формуле ∫udv=u*v-∫vdu; ∫㏑хdx, здесь u=㏑x⇒du=dx/x; dv=dx⇒v=x.
∫3㏑хdx=3*∫㏑хdx=3*(x*㏑x-∫x*dx/x)=3*(x*㏑x-x)+c₁
Справа табличный интеграл dy/sin²у=-сtgy+c₂
3*(x*㏑x-x)+c₁=-сtgy+c₂⇒сtgy=c₂-c₁-3*(x*㏑x-x)
y=arcctg((c-3*(x*㏑x-x)); c=-c₁+c₂
-
Автор:
rangeranda - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
найдите первообразную для функции f(x)=x^2-sinx
-
Предмет:
Математика -
Автор:
parisbuckley - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Сила тока в цепи 15 А, общее сопротивление 540 Ом. Последовательно включены две лампы по 150 Ом каждая, и реостат. Определите сопротивление реостата и силу тока
-
помогите пожалуйста 2sin^2x-√3sinx=0
-
Предмет:
Математика -
Автор:
glennbernard - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Помогите, нужно написать формулы через которые решать и решить
How much to ban the user?
1 hour
1 day
100 years
