Задать вопрос Регистрация
Помочь другим

  • Помогите решить.желательно с полным расписанием решения и коммментариями.

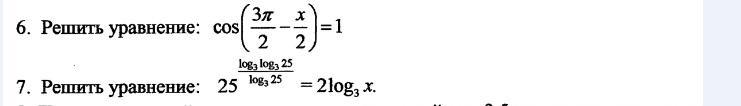
    question img

Ответы 9

  • А по какому принципу решено второе уравнение ?

    • Автор:

      suarez
    • 5 лет назад
    • 0
  • Сначала была использована формула частного логарифмов с одинаковым основанием. Затем можно заметить, что в получившемся выражении основание логарифма и основание степени одинаковы, что дает нам возможность сделать то, что мы сделали. Если коротко - эти действия можно найти в таблице с логарифмическими формулами

    • Автор:

      pacogkvw
    • 5 лет назад
    • 0
  • А как насчёт того, что икс должен быть больше нуля?
  • Т.е данное решение не верное ? а как же тогда решить?

    • Автор:

      beetle
    • 5 лет назад
    • 0
  • А по какому принципу решено первое уравнение ?
  • Сначала использованы формулы приведения :Cos(3pi/2-x) = - Sinx , а потом частный случай для решения тригонометрического уравнения с синусом .

    • Автор:

      viola54
    • 5 лет назад
    • 0
  • Действительно, корень -5 не входит в область допустимых значений, упустил этот момент, спасибо

  • ####################

    answer img

    • Автор:

      zoe
    • 5 лет назад
    • 0

  • 6)Cos(\frac{3\pi }{2} -\frac{x}{2})=1\\\\-Sin\frac{x}{2}=1\\\\Sin\frac{x}{2}=-1\\\\\frac{x}{2}=-\frac{\pi }{2}+2\pi n,n\in Z\\\\x=-\pi+4\pi n,n\in Z

    7) ОДЗ : x > 0

    25^{\frac{log_{3}log_{3}25}{log_{3}25}} =2log_{3}x

    По свойству логарифмов :

    log_{a}b=\frac{log_{c}b }{log_{c}a }

    получим, что :

    \frac{log_{3}log_{3}25}{log_{3}25}=\frac{log_{25}log_{3}25}{log_{25}25}=\frac{log_{25}log_{3}25}{1}=log_{25}log_{3}25

    Следовательно :

    25^{log_{25}log_{3}25}=2log_{3}x\\\\log_{3}25=log_{3}x^{2}\\\\25=x^{2}\\\\x_{1}=5\\\\x_{2}=-5<0\\\\Otvet:5

    answer img

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years