-
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x1, x2, ..., x9. Среди этих точек найдите все точки, в которых производная функции y = f(x)
1)Все точки в которых производная равна нулю
2Все точки в которых производная наибольшая
В ответе укажите количество найденных точек.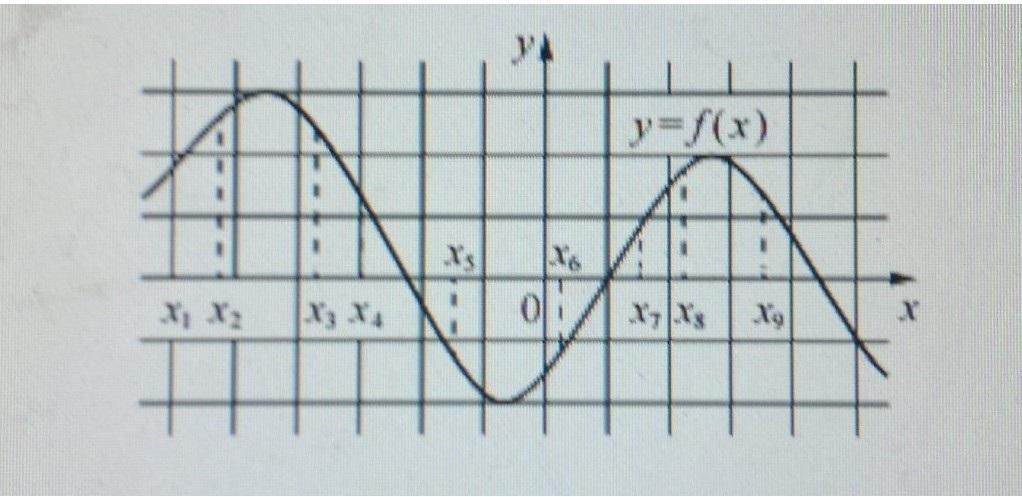
-
Предмет:
Математика -
Автор:
pepearias - 6 лет назад
-
Ответы 1
-
Ответ:
1)нет таких точек, т.е. 0; 2) 1 точка х7
Пошаговое объяснение:
Геометрически производная -это тангенс угла наклона касательной в заданной точке. Значит:
1)производная =0 в вершинах и впадинах графика, где касательная горизонтальна, а ни одна точка там не находится;
2)производная максимальна там, где самый крутой наклон, примерно при х=-2.5, +1, +3.5 деления, и опять -ни одна точка там не отмечена. Если сравнивать между собой, как в условии, то самая крутая, пожалуй х7 (надо приложить линейку и аккуратно, слегка наметить карандашом касательные в каждой точке, и сравнить углы наклона. По фото это только на глазок можно сделать)
-
Автор:
doodlesjennings - 6 лет назад
-
0
-
-
Добавить свой ответ
-
НАЙДИТЕ ПРОИЗВОДНУЮ ФУН-И f(X)=X^7\7+7X^3+X+8 ПРИ ВЫЧИСЛЕНИИ X=-1
-
Предмет:
Математика -
Автор:
fisherbrandt - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
дайте названия для 3,3 диметил бутена 1
-
Предмет:
Химия -
Автор:
winniebibr - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Напишите все двузначные числа, для записи которых используются только 0, 1, 6, 8. подчеркните те из них которые кратны 2
-
Предмет:
Математика -
Автор:
anisevvst - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
радиус уверенного приема телепрограмм от останкинской телевизионной башни в москве составляет 130км за какое время радиосигнал проходит это расстояние
-
Предмет:
Физика -
Автор:
kellentownsend - 6 лет назад
-
Ответов:
1 -
Смотреть
-
