-
Общим решением дифференциального уравнения ... является ...
Дайте пожалуйста полный ответ :)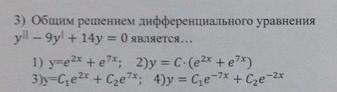
-
Предмет:
Математика -
Автор:
gustavomiles - 6 лет назад
-
Ответы 1
-
Решим соответствующее однородное уравнение y''-3y'+2y=0
Составим характеристический многочлен
k^2-3k+2=0
k1=1 k2=2, оба кратности 1
Общее решение однородного уравнения
y1=C1*e+C2*e^2
Найдем частное решение исходного неоднородного уравнения методом неопределенных коэффициентов
z=2+0i
z=k2=>ищем частное решение в виде
y2=x*(Ax+B)e^2x=e^2x(Ax^2+Bx)
y2'=2e^2x(Ax^2+Bx)+e^2x(2Ax+B)=e^2x(2Ax^2+2(B+A)x+B)
y2''=2e^2x((2Ax^2+2(B+A)x+B)+e^2x(4Ax+2(A+B))
Подставим в исходное уравнение
2e^2x((2Ax^2+2(B+A)x+B)+e^2x(4Ax+2(A+B))-3*(2e^2x(Ax^2+Bx)+e^2x(2Ax+B)=e^2x(2Ax^2+2(B+A)x+B))+2*(e^2x(Ax^2+Bx))=xe^2x
A=1/2
B=-1
y2=(x^2*e^2x)/2-xe^2x
Решение исходного неоднородного уравнения
y=y1+y2=C1*e+C2*e^2+(x^2*e^2x)/2-xe^2x
-
Автор:
Fedoseewa27 - 2 года назад
-
0
-
-
Добавить свой ответ
-
найдите диагонали Паралелепипеда по трём его измерениям 2;2;1
-
Предмет:
Математика -
Автор:
hugo99 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите упростить пример [tex]a^{2} *b\\ a^{2} -2ab[/tex]
-
Предмет:
Алгебра -
Автор:
aidenmoore - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Чему равна среднеквадратичная скорость молекул радона Rn, если его температура равна 153
ºС?
-
♂️♂️♥️♥️♥️
Произвести акустический расчет для зала заседаний и рассчитать систему
для усиления речи.
Данные для расчета:
Число слушателей 340 человек.
План и вертикальный разрез помещения приведены на рис. 3.
Требуемый уровень звукового поля 80 дб.
Допустимая неравномерность поля уровней прямого звука б дб.
Определить: Построить честотные характеристики времени реверберации
(Топт, Трас) и индекс усиления
-
Предмет:
Физика -
Автор:
verónicatate - 6 лет назад
-
Ответов:
1 -
Смотреть
-
