Задать вопрос Регистрация
Помочь другим

  • 70 Б. Здравствуйте. Ищу помощи с решением уравнения! Найти общий интеграл однородного дифференциального уравнения первого

    порядка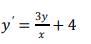

    question img

Ответы 1

  • Первый способ.

    Так как диф. уравнение однородное, то для него осуществляется замена y = ux, тогда y' = u'x + u, имеем:

    u'x+u=3u+4~~~\Rightarrow~~~ u'x=2u+2~~~\Rightarrow~~~ \displaystyle \int\dfrac{du}{u+1}=\int \dfrac{2dx}{x}\\ \\ \\ \ln|u+1|=\ln |x^2|+\ln C~~~\Rightarrow~~~ u+1=Cx^2~~~\Rightarrow~~~ u=Cx^2-1

    Выполнив обратную замену u = y/x, имеем:

    \dfrac{y}{x}=Cx^2-1~~~~\Rightarrow~~~~\boxed{\dfrac{y}{x^3}+\dfrac{1}{x^2}=C}

    Получили общий интеграл.

    Второй способ.

    y'-\dfrac{3y}{x}=4

    Умножим левую и правую части уравнения на \mu (x), которое определяется соотношением:

    \displaystyle \mu (x)=e^{\int-\frac{3}{x}dx}=e^{-3\ln |x|}=\dfrac{1}{x^3}

    \dfrac{y'}{x^3}-\dfrac{3y}{x^4}=\dfrac{4}{x^3}\\ \\ y'\cdot \dfrac{1}{x^3}+y\cdot \left(\dfrac{1}{x^3}ight)'=\dfrac{4}{x^3}~~~~\Rightarrow~~~ \left(y\cdot\dfrac{1}{x^3}ight)'=\dfrac{4}{x^3}

    Проинтегрируем обе части уравнения

    \dfrac{y}{x^3}=\displaystyle \int\dfrac{4}{x^3}dx~~~~\Rightarrow~~~ \dfrac{y}{x^3}=-\dfrac{2}{x^2}+C~~~~\Rightarrow~~~ \boxed{y=Cx^3-2x}

    Получили общее решение.

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years