Задать вопрос Регистрация
Помочь другим

  • 82 Б. Здравствуйте, помогите решать уравнение. Не срочно . Найти общий интеграл уравнения в полных дифференциалах

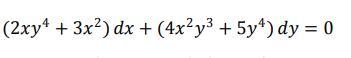
    question img

Ответы 1

  • В уравнении M(x;y)=2xy^4+3x^2;~~ N(x;y)=4x^3y^3+5y^4. Действительно, \dfrac{\partial M}{\partial y}=8xy^3=\dfrac{\partial N}{\partial x}, т.е. дифференциальное уравнение является уравнением в полных дифференциалах.

    Интегрируя по х

    F(x;y)=\displaystyle \int M(x;y)dx=\int(2xy^4+3x^2)dx=x^2y^4+x^3+C(y)

    Теперь эту функцию продифференцируем по у.

    F'_y(x;y)=4x^2y^3+C'(y)

    Видим, что F'_y(x;y)=N(x;y)=5y^4+4x^3y^3 отсюда C'(y)=5y^4, получим C(y)=\displaystyle \int 5y^4 dy=y^5

    Общий интеграл:   y^5+x^2y^4+x^3=C

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years