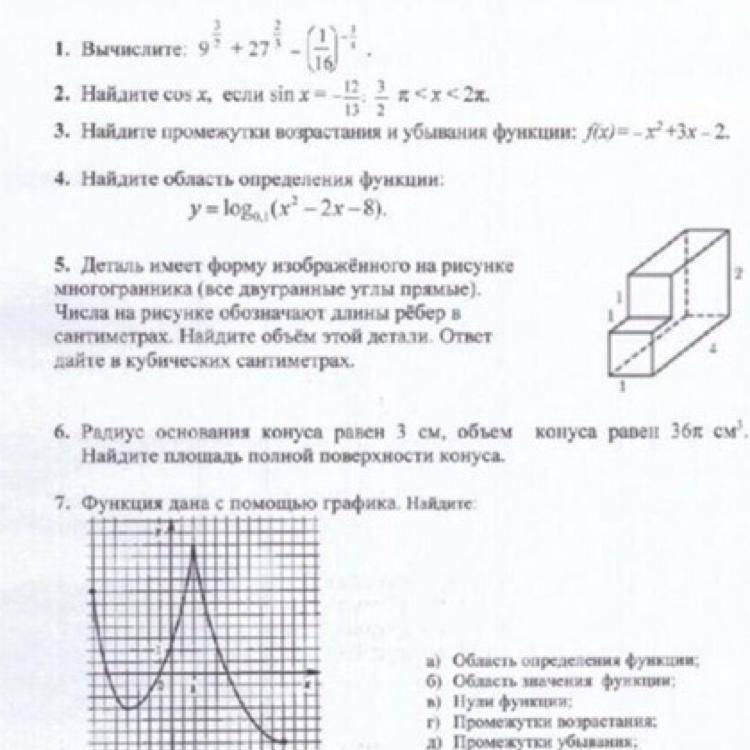
Кто сможет решить 4 и 6 задание?это очень срочно!заранее спасибо!

Логарифмическая функция определена только для положительных аргументов, поэтому выражение под знаком логарифма должно быть больше нуля:

x^2 - 2x - 8 > 0.

Чтобы найти интервалы, где это неравенство выполняется, решим его с помощью метода интервалов и графически. Сначала найдем корни квадратного уравнения:

x^2 - 2x - 8 = 0.

D = 2^2 - 4*1*(-8) = 36,

x1 = (2 + √36) / 2 = 5,

x2 = (2 - √36) / 2 = -3.

Корни уравнения разбивают вещественную ось на три интервала: (-∞, -3), (-3, 5), (5, +∞).

Выберем по одной точке из каждого интервала и подставим их в неравенство, чтобы определить знак выражения x^2 - 2x - 8 на каждом интервале:

-4: (-4)^2 - 2*(-4) - 8 = 0 > 0,

0: 0^2 - 2*0 - 8 = -8 < 0,

6: 6^2 - 2*6 - 8 = 20 > 0.

Таким образом, неравенство x^2 - 2x - 8 > 0 выполняется на интервалах (-∞, -3) и (5, +∞). Ответом будет:

D = (-∞, -3) ∪ (5, +∞).

Область определения функции y = log (x^2 - 2x - 8) равна D = (-∞, -3) ∪ (5, +∞).

Объем конуса можно выразить через радиус основания R и высоту h:

V = (1/3) π R^2 h,

где π - число пи.

Выразим высоту конуса h через его объем V:

h = (3V) / (πR^2).

Подставляя значение объема V = 36 л = 36000 см^3 и радиуса основания R = 3 см, получаем:

h = (3 36000 см^3) / (π 3^2 см^2) ≈ 1212,96 см.

Теперь, чтобы найти площадь полной поверхности конуса, нужно вычислить боковую поверхность и добавить к ней площадь основания.

Площадь основания конуса равна:

Sосн = π R^2 = π 3^2 см^2 ≈ 28,27 см^2.

Боковая поверхность конуса состоит из сектора круга и равнобедренного треугольника. Угол сектора можно найти из соотношения:

V = (1/3) π R^2 h = (1/3) π R^2 √(h^2 + R^2),

откуда:

tan(α) = R / h.

Поэтому:

α = arctan(R / h) ≈ 0,147 рад.

Длина окружности основания равна:

L = 2πR = 6π см.

Длина боковой стороны равнобедренного треугольника:

l = √(h^2 + R^2) ≈ 1213,68 см.

Площадь сектора круга:

Sсек = (1/2) R^2 α = (1/2) 3^2 см^2 0,147 ≈ 0,66 см^2.

Площадь равнобедренного треугольника:

Sтр = (l/2) √(R^2 - (l/2)^2) ≈ 108,78 см^2.

Таким образом, площадь боковой поверхности конуса:

Sбок = Sсек + Sтр ≈ 109,44 см^2.

Итого, площадь полной поверхности конуса:

S = Sосн + Sбок ≈ 137,71 см^2.

Ответ: площадь полной поверхности конуса равна примерно 137,71 см^2.