Задать вопрос Регистрация
Помочь другим

  • Исследуйте ряд на сходимость (если что "n+1" в скобках)

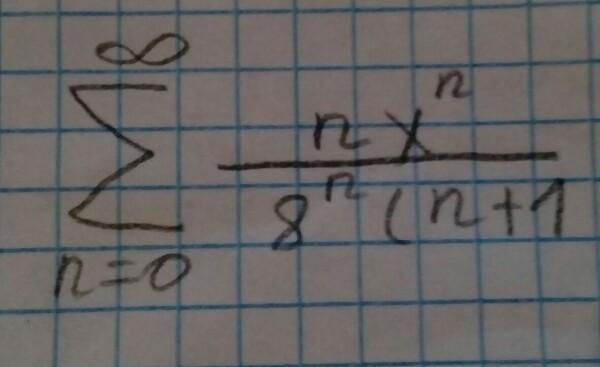
    question img

Ответы 2

  • Сейчас дорешаю, а то плохо видно

  • Ответ:

    область сходимости x \in (-8;8)

    Пошаговое объяснение:

    \sum\limits_{n=0}^\infty\frac{nx^n}{8^n(n+1)} - функциональный степенной ряд

    Пусть  \bigg|u_n(x)\bigg|=\frac{n\big|x^n\big|}{8^n(n+1)}, Пусть  \bigg|u_{n+1}(x)\bigg|=\frac{(n+1)\big|x^{n+1}\big|}{8^{n+1}(n+2)}

    Найдём предел: \lim\limits_{n \to \infty}\bigg|\frac{u_{n+1}}{u_{n}}\bigg|= \lim\limits_{n \to \infty}\Bigg(\frac{(n+1)\big|x\big|^{n+1}}{8^{n+1}(n+2)}} \times \frac{8^n(n+1)}{n\big|x\big|^n}\Bigg)

    = \frac{\big|x\big|}{8}

    \big|x\big|<8\\-8<x<8

    Пусть x=8

    \sum\limits_{n=0}^\infty\frac{n8^n}{8^n(n+1)} - знакоположительный ряд

    \sum\limits_{n=0}^\infty\Bigg(1-\frac{1}{(n+1)}\Bigg) - ряд расходится по достаточному признаку расходимости, т.к. предел равен 1

    Пусть x=-8

    \sum\limits_{n=1}^\infty\frac{n(-1)^n8^n}{8^n(n+1)} - знакочередующийся ряд.ряд расходится по достаточному признаку расходимости, т.к. предел равен 1

    Ответ: область сходимости x \in (-8;8)

    • Автор:

      piper93
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years