-
помогите с логарифмами пожалуйста, как решать их? в инете непонятно, сложно
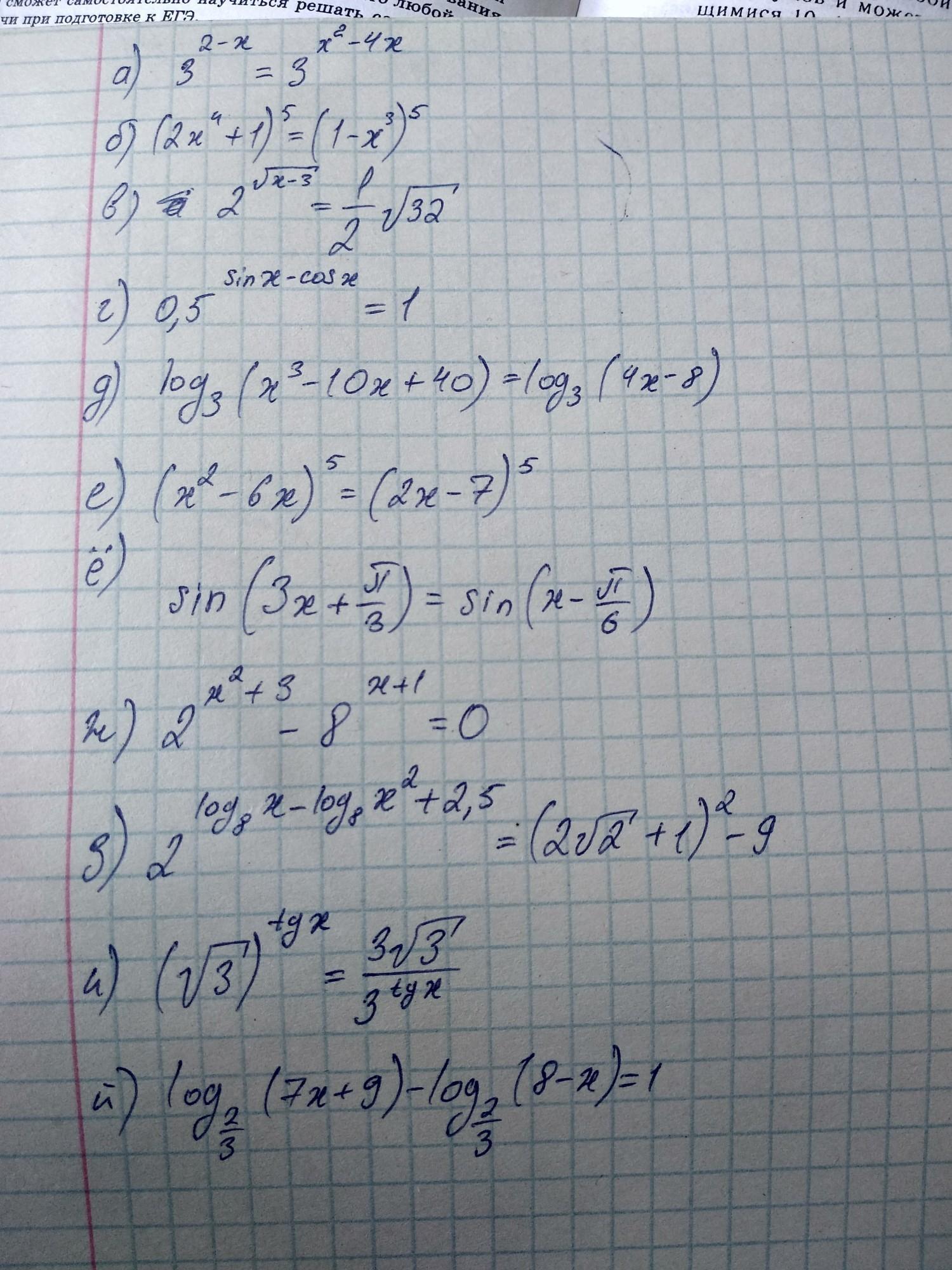
-
Предмет:
Математика -
Автор:
elliotmann - 6 лет назад
-
Ответы 1
-
-
Автор:
arianna - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
1. Инструмент и инвентарь относят к оборотным фондам по двум признакам
a) оплате и внешному виду
b) работоспособности
c) внешнему виду и работоспособности
d) стоимости и сроку службы
2. Какое предпринимательство можно назвать ведущим видом предпринимательство?
a) финансовое
b) консультативное
c) коммерческое
d) производственное
3. Что не относится к передаточным устройствам?
a) линии электропередач
b) шнуры
c) Газопроводы
d) силовые кабели
4. Что является основным принципом теории динамического неравновесия?
a) динамичность
b) практичность
c) инновационность
d) дисциплина
5. Предприниматель не имеет право
a) Устанавливать на нее цены по своему усмотрению не взирая на закон РФ
b) самостоятельно формировать производственную программу выбирать поставщиков и потребителей своей продукции и Устанавливать на нее цены по своему усмотрению не взирая на закон РФ
c) Осуществлять внешне экономическую деятельность
d) привлекать на договорных началах и использовать финансовые средства объекты интеллектуальной собственности имущество и отдельные имущественные права граждан и юр лиц -
помогите написать эссе на тему наша школа будущего
-
Предмет:
Русский язык -
Автор:
spicyjrww - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Инструмент и инвентарь относят к оборотным фондам по двум признакам
a. оплате и внешнему виду
b. работоспособности
c. внешнему виду и работоспособности
d. стоимости и сроку службы
Что не входит в число факторов производства?
a. документация
b. производственные фонды
c. рабочая сила
d. информация
Вопрос 3
Какое предпринимательство получило наибольшее развитие в первые годы перехода к рынку в России?
a. государственное
b. частное
c. частное и коммерческое
d. коммерческое
Вопрос 4
Какое предпринимательство получает в последние годы всё большее развитие в России?
a. консультативное
b. коммерческое
c. производственное
d. финансовое
Вопрос 5
Какие отношения порождают у многих граждан естественное стремление иметь «свое дело»?
a. рыночные
b. политические
c. социальные
d. экономические
Вопрос 6
Что такое сфера финансовой деятельности?
a. общение, финансирование
b. финансирование
c. обращение, обмен стоимостей
d. обмен валютами
Вопрос 7
Субъектами предпринимательства не могут быть:
a. граждане иностранных государств и лица без гражданства в пределах полномочий, установленных законом
b. объединения граждан (партнеры)
c. граждане РФ и других государств, не ограниченные в установленном законом порядке в своей деятельности
d. только граждане своей страны
Вопрос 8
Кто был автором выражения «Предприниматель — энергичный человек, действующий в условиях умеренного риска»?
a. Макс Вебер
b. Ф. Найт
c. Иозеф Шумпетер
d. Дэвид Макклелланд
Вопрос 9
К основным задачам, которые нужно решать в начале предпринимательской деятельности не относятся
a. выбор местоположения фирмы
b. выбор формы предпринимательской деятельности
c. финансирование и инвестирование
d. отбор кадров
Вопрос 10
Что является основным принципом теории динамического неравновесия?
a. инновационность
b. динамичность
c. практичность
d. дисциплина -
Определить направления выпоклости и точки перегиба графика функции
[tex]f(x) = {3x}^{5} - {5x}^{4} + 3x - 2[/tex]
-
Предмет:
Математика -
Автор:
zoiehr7m - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
