Задать вопрос Регистрация
Помочь другим

  • помогите проверить на сходимость числовой ряд
    фото в приложении​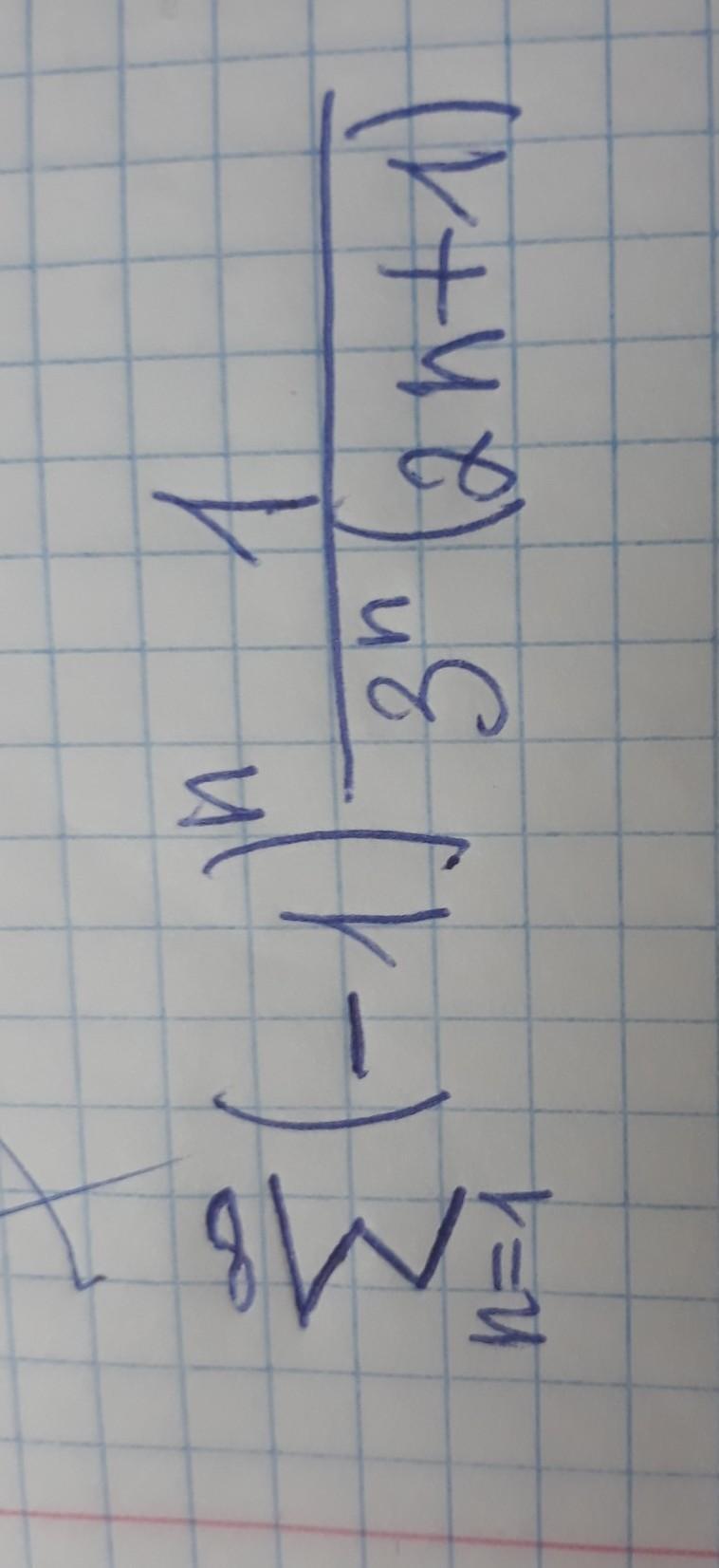

    question img

Ответы 1

  • По первому признаку Лейбница каждый последующий член ряда по абсолютной величине меньше предыдущего, т.е.

    1/9 > 1/45 > 1/189 >...

    \displaystyle \lim_{n \to \infty}\frac{1}{3^n(2n+1)}=0

    Второе условие признака Лейбница тоже выполняется.

    Значит ряд сходится. Теперь проверим на абсолютность или условной сходимости. Возьмём ряд по модулю, имеем

    \bigg|\displaystyle\sum^{\infty}_{n=1}\frac{(-1)^n}{3^n(2n+1)}\bigg|=\sum^{\infty}_{n=1}\frac{1}{3^n(2n+1)}

    По признаку Даламбера

    \displaystyle \lim_{n \to \infty}\frac{3^n(2n+1)}{3^{n+1}(2(n+1)+1)}=\frac{1}{3}\lim_{n \to \infty}\frac{2n+1}{2n+3}=\frac{1}{3}<1

    Следовательно, данный ряд сходится абсолютно.

    • Автор:

      teagan
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years