-
[Умоляю!]
Решите систему неравенств на фото!
Даю (100) баллов!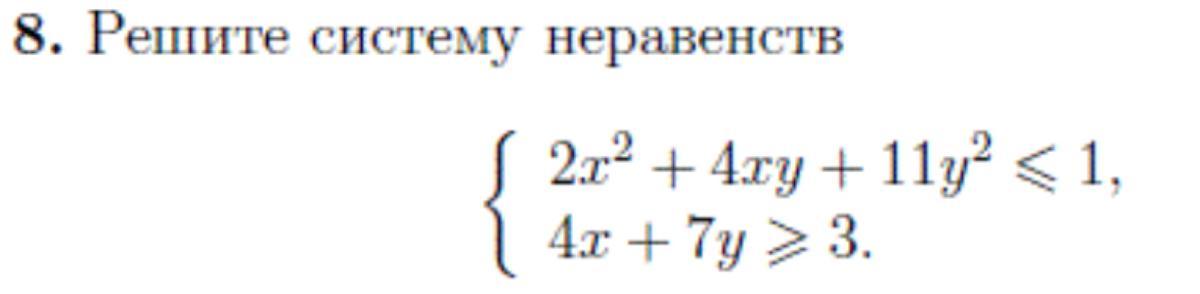
-
Предмет:
Математика -
Автор:
maliyaho5xl - 6 лет назад
-
Ответы 1
-
Пусть x = 3k, y = 3m. Тогда
Ответ:
-
Автор:
pongomcmahon - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Вставить is/isn't, are/aren't,am/'m not.
1. I ______ lazy
2. My friend ________ naughty.
3.My granny _______ kind.
4.My granddad _______ clever.
5. My teachers ________ funny.
6.I _______ a bad pupul-
Предмет:
Английский язык -
Автор:
henrybennett - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Яким був суспільно-політичний рух в Україні другої половини 16 століття на початку 17 століття
-
Дам 20 баллов!
Решить неравенство
1. ( x-7)(x+8)>0
2. 2^(1-x)<4
Найти производную функцию
y=-2x^2+3x в точке x_0=-3
[tex](x-7)(x+8)\ \textgreater \ 0\\2^{1-x} \ \textless \ 4\\\\y=-2x^2+3x \\x_0=-3[/tex]-
Предмет:
Математика -
Автор:
buzzyarnold - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Конспект с планом. Методы исследования Биологии. 8 класс.
Помогите,пожалуйста. 30б-
Предмет:
Биология -
Автор:
hassantnao - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
