Найдите площадь фигуры, состоящей из всех точек плоскости, координаты которых удовлетворяют системе неравенств

{ |x|+|y|<4

{ |y|<1

{ |x| + |y| < 4

{ |y| < 1

Так как |x| >= 0 и |y| >= 0, то ясно, что:

{ y Є (-1; 1) - это бесконечная полоса между прямыми y = -1 и y = 1

{ |x| < 4; x Є (-4; 4)

{ x Є (-4; 4) - это бесконечная полоса между прямыми x = -4 и x = 4.

{ y Є (-1; 1) - это бесконечная полоса между прямыми y = -1 и y = 1

Но есть еще отрезки прямых:

y = x + 4; y = x - 4; y = -x + 4; y = -x - 4

Они тоже ограничивают область, чтобы, например, точка (4, 1) не попала.

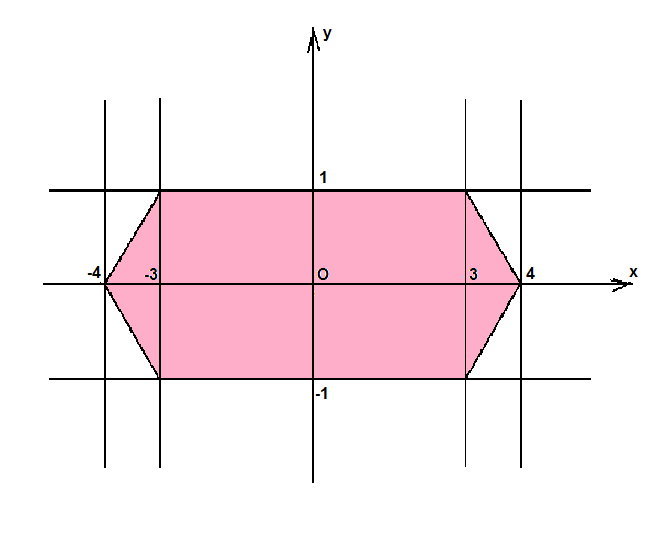
Примерный график показан на рисунке. Нужная Площадь закрашена.

Она состоит из:

1) Прямоугольника от -3 до 3 по оси Ox и от -1 до 1 по оси Oy.

Площадь этого прямоугольника S1 = 6*2 = 12

2) Двух треугольников, от -4 до -3 и от 3 до 4 по оси Ox и от -1 до 1 по оси Oy.

Площадь каждого из них S2 = 2*1/2 = 1

Суммарная площадь равна:

S = S1 + 2*S2 = 12 + 2*1 = 14