-
Помогите пожалуйста решить логарифм.
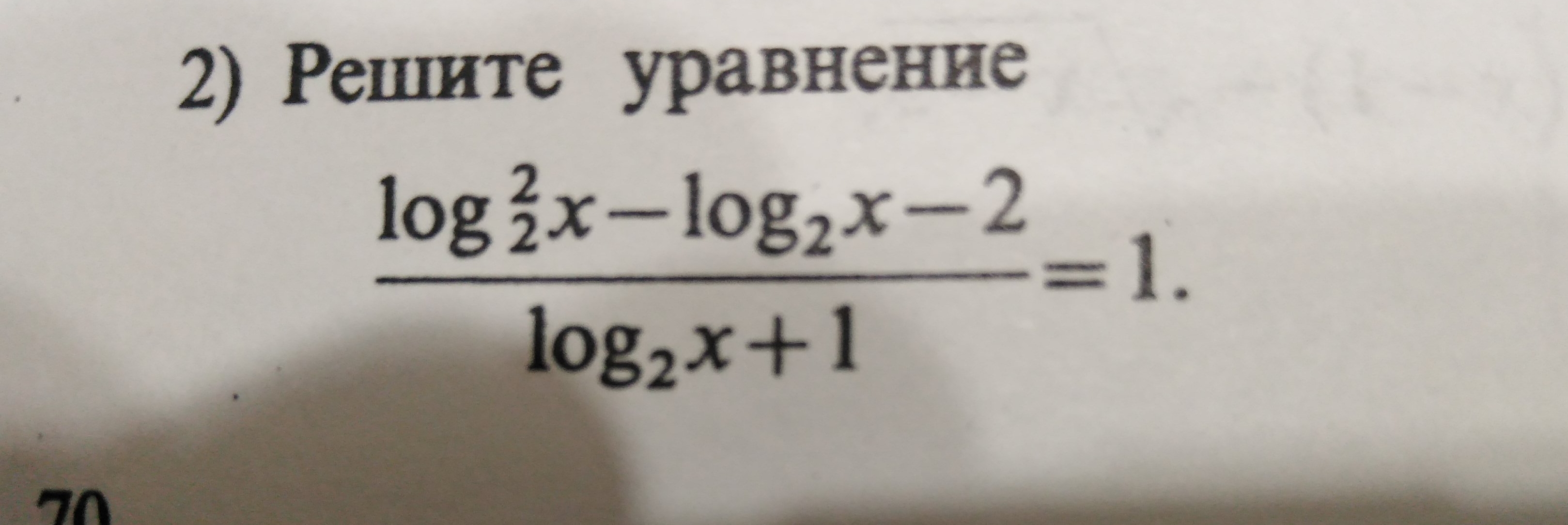
-
Предмет:
Математика -
Автор:
ninali0912 - 3 года назад
-
Ответы 1
-
{(x–1)(x2+2)>0 ⇒ x–1>0 ⇒ x>1
{x2+3x–4>0 ⇒ D=9+16=26; x=(−3±5)
2
; x<–4 или x>1
{x>0
так как 1=log22
Перепишем неравенство:
log2(x–1)(x2+2) +log2x≤ log22+log2(x2+3x–4)
Заменим сумму логарифмов логарифмом произведения
log2x·(x–1)·(x2+2) ≤ log22·(x2+3x–4)
Логарифмическая функция с основанием 2 >1 возрастает, значит
бОльшему значению функции соответствует бОльшее значение аргумента
x·(x–1)·(x2+2) ≤ 2·(x2+3x–4)
х·(х–1)·(x2+2)–2·(x–1)(x+4) ≤ 0
(x–1)·(x3+2x–2x–8) ≤ 0
(x–1)·(x3–8) ≤ 0
(x–1)·(x–2)·(x2+2x+4) ≤ 0
(x–1)(x–2) ≤ 0
__+_ [1] _–_ [2] _+__
x ∈ [1;2]
C учетом ОДЗ получим
о т в е т.(1;2]
-
Автор:
OldHack - 3 года назад
-
9
-
-
Добавить свой ответ
Еще вопросы
-
Какие основные группы программного обеспечения принято выделять по функциональному назначению
-
Предмет:
Русский язык -
Автор:
phoenixmichael - 3 года назад
-
Ответов:
1 -
Смотреть
-
-
ДАЮ 5 баллов. Помогите по литературе.
-
Предмет:
Литература -
Автор:
kamrynbowman - 3 года назад
-
Ответов:
4 -
Смотреть
-
-
"Кто не добрый тот злой". Какой знак препинания нужно поставить перед "тот"?
-
Предмет:
Русский язык -
Автор:
edgarwarner - 3 года назад
-
Ответов:
1 -
Смотреть
-
- 3 примера по алгебре. Помогите пожалуйста
How much to ban the user?
1 hour
1 day
100 years
