-
Докажите, что прямая = 3 − 2, = −4, = 4 + 1 параллельна плоскости4 − 3 − 6 + 3 = 0.
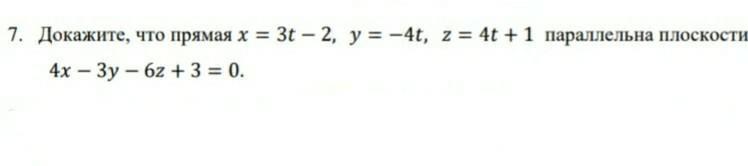
-
Предмет:
Математика -
Автор:
addisyncollier - 3 года назад
-
Ответы 1
-
Уравнение прямой выразим в каноническом виде.
x = 3t – 2, x + 2 = 3t, t = (x + 2)/3.
y = -4t, t = y/(-4).
z = 4t +1, z – 1 = 4t, t = (z – 1)/4.
Получаем уравнения:
(x + 2)/3 = y/(-4) = (z – 1)/4.
Отсюда определяем направляющий вектор заданной прямой.
n = (3; -4; 4).
Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.
Нормальный вектор плоскости снимаем с её уравнения.
N = (4; -3; -6).
Находим скалярное произведение этих векторов.
nxN = 3*4 + (-4)*(-3) + 4*(-6) = 12 + 12 – 24 = 0.
Доказана параллельность.
-
Автор:
mini skirt08rf - 3 года назад
-
7
-
-
Добавить свой ответ
-
яка довжина бороди була у дідка який викрав королівну
-
Предмет:
Українська література -
Автор:
gemma - 3 года назад
-
Ответов:
1 -
Смотреть
-
-
записать глаголы в изъявит, условном, повелительном наклонении: лечить, купить,возить, учить, хвалить, просить, мыть,
Пример: лечить-лечит, лечил бы, лечи.
Пример: ждать- жду, ждал бы, жди.
Пожалуйста!! даю 30 баллов
-
Предмет:
Русский язык -
Автор:
piper - 3 года назад
-
Ответов:
1 -
Смотреть
-
-
найдите сумму чисел, которые больше или равно -5, но меньше -3
-
Предмет:
Математика -
Автор:
briley - 3 года назад
-
Ответов:
1 -
Смотреть
-
-
як козаки виловлювали татар?
"за сестрою"
-
Предмет:
Українська література -
Автор:
edmundo - 3 года назад
-
Ответов:
1 -
Смотреть
-
