-
линейная алгебра
1. Вычислить расстояние между точками А(9:-2) и В(7;1).
2 . В пространстве даны точки А(5;2;-8), В(6:2;4), С(0;6;-6). Вычислить косинус угла ВАС.
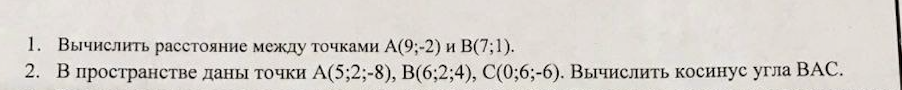
-
Предмет:
Математика -
Автор:
esoo - 3 года назад
-
Ответы 1
-
1)Чтобы найти расстояние между точками A и B, зная их координаты, необходимо из конечной точки В вычесть соответствующие координаты начальной точки А. То есть: AB = Bх - Aх.
Подставим значения координат точки А ( -7,3) и точки В ( -2):
AB = -2 - ( -7,3) (так как перед скобкой отрицательный знак, то при раскрытии скобок поменяем знаки в скобках на противоположные знаки) = -2 + 7,3 = 5,3.
Подставим значения координат точки А ( -8,4) и точки В ( -3,5):
AB = -3,5 - ( -8,4) = -3,5 + 8,4 = 4,9.
Ответ: расстояние между точками А ( -7,3) и В ( -2) составляет 5,3 единицы; между точками А ( -8,4) и В ( -3,5) составляет 4,9 единиц
2)Угол С - это угол между векторами СА и СВ.
1. Определим координаты вектора СА:
СА = (- 1 - 0; 3 - (- 2); - 5 - (- 5)) = (- 1; 5; 0).
Определим координаты вектора СВ:
СВ = (4 - 0; 2 - (- 2); - 5 - (- 5)) = (4; 4; 0).
2. Найдем скалярное произведение векторов СА и СВ:
СА*СВ = (-1)*4 + 5*4 + 0*0 = - 4 + 20 + 0 = 16.
3. Скалярное произведение двух векторов равно произведению их длин на косинус угла между ними.
Найдем длину вектора СА:
|СА| = √((-1)^2 + 5^2 + 0^2) = √(1 + 25 + 0) = √26.
Найдем длину вектора СВ:
|СВ| = √(4^2 + 4^2 + 0^2) = √(16 + 16 + 0) = √32.
4. Таким образом:
|СА|*|СВ|*cosC = СА*СВ;
√26 * √32 * cosC = 16;
cosC = 16/√832 = 16/√16*4*13 = 16/4*2√13 = 16/8√13 = 2/√13 = 2√13 / 13.
Ответ: cosC = 2√13 / 13.
-
Автор:
Fedoseewa27 - 3 года назад
-
0
-
-
Добавить свой ответ
-
Очень нужна помощь с химией
-
Предмет:
Химия -
Автор:
harrisonr61z - 3 года назад
-
Ответов:
1 -
Смотреть
-
-
Помогите с физикойй
-
Предмет:
Физика -
Автор:
annbautista - 3 года назад
-
Ответов:
1 -
Смотреть
-
-
Помогите решить!!! Причастия 7 класс
-
Предмет:
Русский язык -
Автор:
beatricexs77 - 3 года назад
-
Ответов:
1 -
Смотреть
-
- 2. Магматичне походження мають наступні корисні копалини: А. нафта, кам'яна сіль, вапняк, торф, пісок Б. титанові руди, граніт, залізні руди, базальт В. вугілля, графіт, алмази, мармур, вапняк Помогите осталось 10 минут
