-
Помогите пожалуйста вычислить интегралы. Те, что обведены кружками
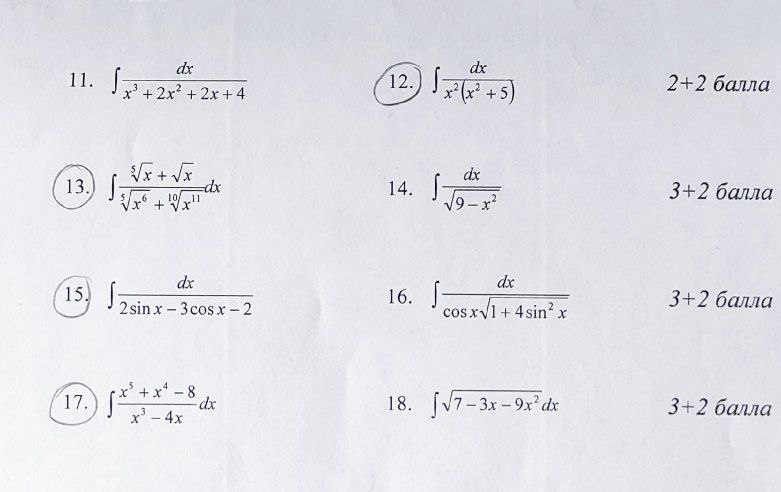
-
Предмет:
Математика -
Автор:
sullivanydmc - 3 года назад
-
Ответы 1
-
12)Можно записать его в таком виде:∫ (1 / x^2 - 1 / {x^2 + 5}) dx / 5Теперь видно, что он разбивается разность табличных интегралов....13)Напрашивается замена:x = t^10Интеграл примет вид:10 ∫ (1 + t^3) dt / (1 + t)Скобочки друг на друга можно поделить, получится:10 ∫ {t^2 - t + 1} dtОн разбивается на сумму интегралов от степенных функций и от константы....15)Универсальная триганометрическая тут вполне подойдет:tg(x / 2) = tИнтеграл примет вид:- 2 ∫ dt / {2 (t - 1)^2 + 3}Дальше он легко приводится к табличному виду....17)Выражение:1 / {x^3 - 4x}можно переписать так:(1 / 8) (1 / {x - 2} + 1 / {x + 2} - 2 / x)Тогда исходный интеграл можно будет расписать как сумму трех интегралов:(1 / 8) ∫ (x^5 + x^4 - 8) dx / (x - 2) ++ (1 / 8) ∫ (x^5 + x^4 - 8) dx / (x + 2) +- (1 / 4) ∫ (x^5 + x^4 - 8) dx / x Первый интеграл: замена x = t + 2, и он превратится в сумму степенных интегралов.Второй интеграл: замена x = t - 2, и он превратится в сумму степенных интегралов.Третий интеграл: а он и так норм, уже можно представить в виде суммы степенных.
-
Автор:
joaquímclf4 - 3 года назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
как зовут капитанскую дочку?
-
Предмет:
Литература -
Автор:
jaidyn50 - 3 года назад
-
Ответов:
1 -
Смотреть
-
-
Сколько будет 1+1 помогите пожалуйста
-
Предмет:
Математика -
Автор:
blake7 - 3 года назад
-
Ответов:
1 -
Смотреть
-
-
Помогите!!!Соч 1 вариант 2 задание Найдите среди чисел 1 2/5;4/15;7/5;3 3/4 взаимо обратные
-
Предмет:
Математика -
Автор:
tammy - 3 года назад
-
Ответов:
1 -
Смотреть
-
-
Геометрия, 8 класс. Соч за вторую четверть (задание 3)
-
Предмет:
Геометрия -
Автор:
maximilian88 - 3 года назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
