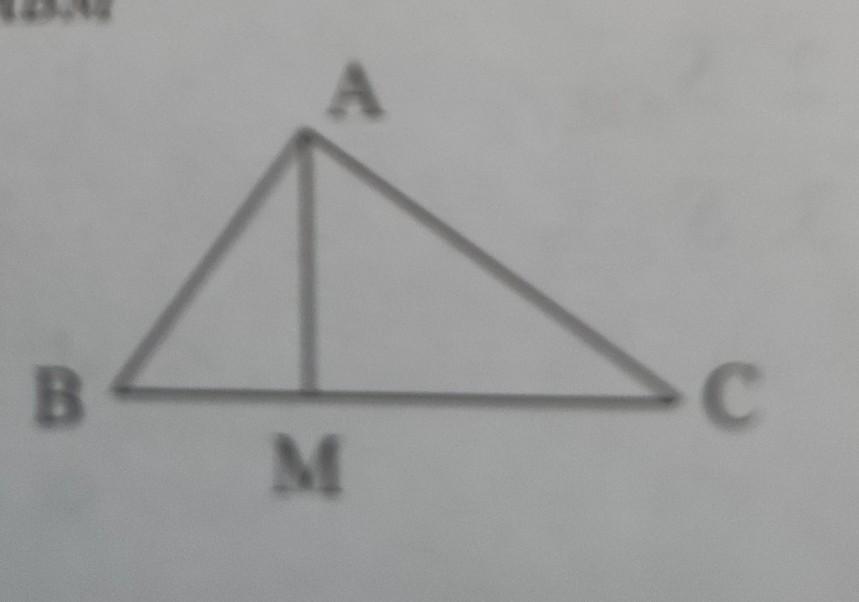
. Найдите площадь треугольника АВС, если BM:MC=2:3 и SAABM = 36 см². ​

Для решения этой задачи понадобится формула для площади треугольника по его высоте:

S = (1/2) * b * h

где S - площадь треугольника, b - длина основания треугольника, h - высота треугольника.

Также нам понадобится отношение сторон BM и MC, которое равно 2:3.

Пусть AM = x, тогда MB = 2x и MC = 3x.

Также из условия задачи известна площадь треугольника AABM, которая равна 36 квадратных см.

Используя формулу для площади треугольника по его высоте, можем записать:

36 = (1/2) * AB * BM

AB * BM = 72

Аналогично для треугольника AACM:

S(AACM) = (1/2) * AC * MC

S(AACM) = (1/2) * AC * 3x

S(AACM) = (3/2) * AC * x

Так как треугольники AABM и AACM имеют одну общую высоту AM, то их площади относятся как их основания:

S(AABM) : S(AACM) = BM : MC = 2 : 3

36 : S(AACM) = 2 : 3

S(AACM) = 54 квадратных см

Теперь можно найти площадь треугольника ABC, сложив площади треугольников AABM и AACM:

S(ABC) = S(AABM) + S(AACM)

S(ABC) = 36 + 54

S(ABC) = 90 квадратных см

Ответ: площадь треугольника АВС равна 90 квадратных см.