-
ДОПОМОЖІТЬ БУДЬ ЛАСКАА Розв’язати лінійне диференціальне рівняння першого порядку
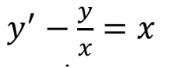
-
Предмет:
Математика -
Автор:
carleyberg - 2 года назад
-
Ответы 1
-
Ответ: Для розв'язання цього диференціального рівняння треба використовувати метод розділення змінних. Записуємо рівняння у вигляді:
dy/dx = y/x
Для того, щоб розділити змінні, перемножимо обидві частини на dx і поділимо на y:
dy/y = dx/x
Зараз можна інтегрувати обидві частини. Інтеграл від лівої частини є натуральним логарифмом, а інтеграл від правої частини є звичайним логарифмом:
∫ dy/y = ∫ dx/x
ln|y| = ln|x| + C
де С - довільна константа інтегрування.
Тепер можна використати властивості логарифмів, щоб отримати вираз для y:
ln|y| = ln|x| + C
|y| = e^(ln|x|+C) = e^C * |x|
y = ± e^C * x
Для визначення константи С потрібно використовувати початкові умови. У цьому випадку немає вказаних початкових умов, тому не можна однозначно визначити значення С. Тому загальний розв'язок має вигляд:
y = ± e^C * x
-
Автор:
dustinxkqw - 2 года назад
-
5
-
-
Добавить свой ответ
-
ПОМОГИТЕ ПЖ, ДАМ 35 БАЛЛОВ
Спишите, вставляя пропущенные буквы и раскрывая скобки.
Сол..це уже к...снулось г...ризонта. Лучи Сол...ца (не)к...саются х...лодной влаги горной реч...ки. На деревьях блестел (вы)павший ночью снег, которого ещё (не)к...снулись яркие лучи зимн...го сол...ца. Волны к...сались скал, где груп...ками с...дели находившиеся птицы. Прик...сновение тёплых капель дождя превратило клумбу (с)цветами в ярк...ю мозаику.
-
Предмет:
Русский язык -
Автор:
cobymeza - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Дано: ∆АВС ∠С=90⁰. Знайти АС і ВС, якщо АВ=13 см, tgA=5⁄12.
-
Предмет:
Математика -
Автор:
tyrell - 2 года назад
-
Ответов:
1 -
Смотреть
-
- Даю 35 балов Доведіть тотожність(n+3)³−(n+3)=(n+2)(n+3)(n+4).
-
250. Велосипедист зі швидкістю велосипедиста їхав 2 год зі швидкістю 18 км/год і 3 год 16 км/год. Знайдіть середню швидкість протягом усього шляху.
-
Предмет:
Математика -
Автор:
konner - 2 года назад
-
Ответов:
1 -
Смотреть
-
