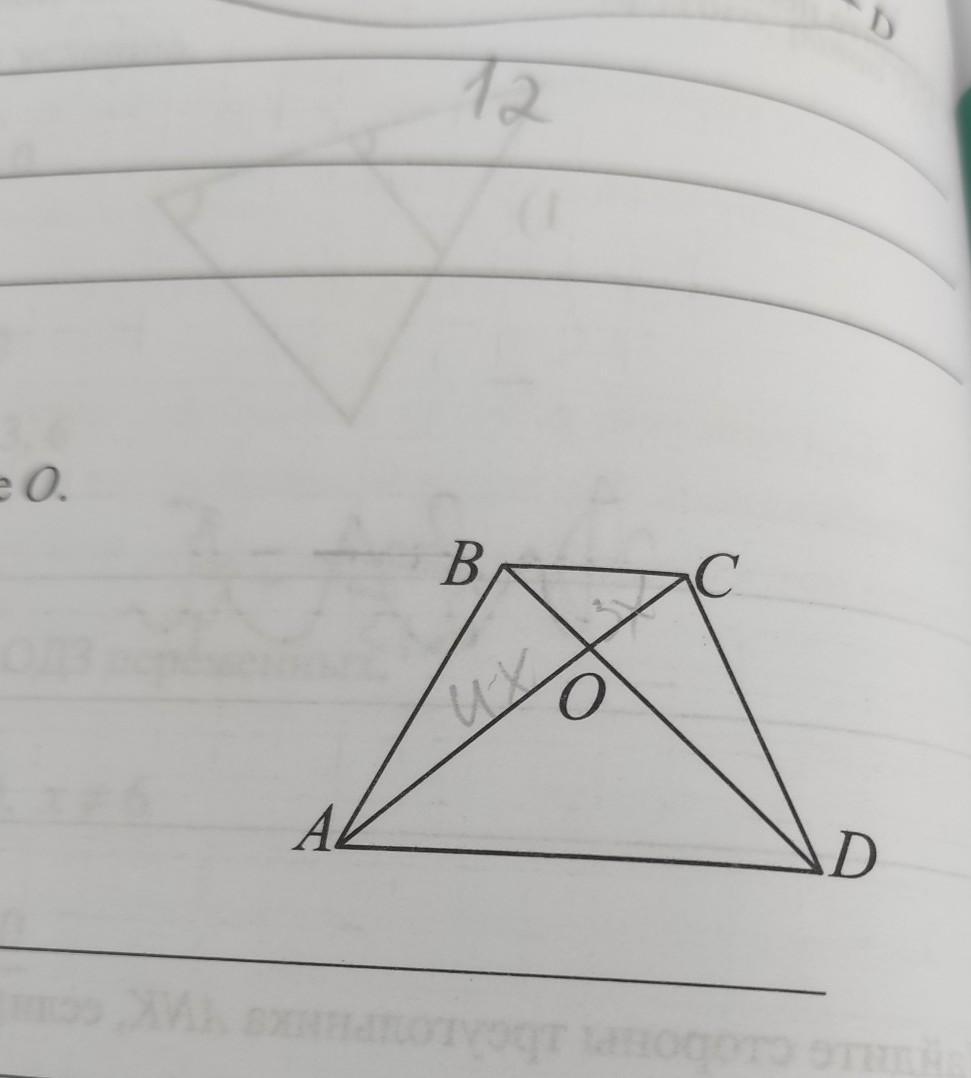
5. Диагонали трапеции ABCD пересекаются в точке О. AD+BC AO 4 Найдите AD-BC если 11 Ос 3 B з AL их DСРОЧНО!!!!!!!!!!​

Ответ:Из условия задачи, мы знаем, что диагонали трапеции ABCD пересекаются в точке O, и что AD + BC = 4.

Также, поскольку AL и BL являются биссектрисами угла A и угла B соответственно, мы знаем, что угол ALO равен углу OLB. Поэтому треугольники ALO и BLO подобны друг другу по признаку угловой сходственности.

Мы можем использовать это свойство, чтобы выразить AD и BC через AO и BL, так как BL является средней линией в треугольнике ABC.

По теореме о средней линии треугольника, BL равна половине суммы оснований AB и CD:

BL = (AB + CD) / 2

Заметим, что AB и CD являются основаниями параллелограмма ABCD, и поэтому равны между собой.

Таким образом, мы можем записать:

BL = (AB + CD) / 2 = (AD + BC) / 2 = 2

По теореме Пифагора в треугольнике ALO:

AL^2 = AO^2 + OL^2

Аналогично, по теореме Пифагора в треугольнике BLO:

BL^2 = BO^2 + OL^2

Подставляя значение BL = 2, получаем:

4 = BO^2 + OL^2

Снова используя свойства подобных треугольников ALO и BLO, мы можем записать:

AD / AO = AO / BD

или

AD = (AO)^2 / BD

и

BC / BO = BO / CD

или

BC = (BO)^2 / CD

Подставляя эти значения в уравнение AD + BC = 4, получаем:

(AO)^2 / BD + (BO)^2 / CD = 4

Заметим также, что по теореме Пифагора в треугольнике ABO:

(AO)^2 + (BO)^2 = AB^2

AB является высотой трапеции ABCD, и поэтому равна:

AB = 2 * OL = 4 / BL = 2

Подставляя это значение в уравнение для AD и BC, получаем:

AD = (AO)^2 / BD = (AO)^2 / (AB + BC) = (AO)^2 / (2 + (BO)^2 / CD)

и

BC = (BO)^2 / CD = (AB^2 - (AO)^2) / CD = (4 - (AO)^2) / CD

Подставляя эти значения в уравнение AD + BC = 4, получаем:

(AO)^2 / (2 + (BO)^2 / CD) + (4 - (AO)^2) / CD = 4

Пошаговое объяснение: