-
Известно, что AC=17 см, AE=14 см, CF=9 см, BD=8 см. Вычислите площадь треугольника ABC! S(АВС)= см2
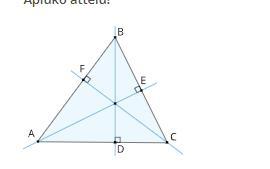
-
Предмет:
Математика -
Автор:
zion64 - 2 года назад
-
Ответы 1
-
воспользуемся формулой Герона для вычисления площади треугольника через длины его сторон:
S = квадратный корень(p(p-a)(p-b)(p-c))
где a, b, c - длины сторон треугольника, а p - полупериметр, равный половине суммы длин сторон:
p = (a + b + c) / 2
Для треугольника ABC нужно найти длины его сторон. Обозначим точку пересечения диагоналей BD и AC как точку M. Поскольку BM делит диагональ AC пополам, то AM = MC = AC / 2 = 8,5 см.
Также заметим, что треугольники AEB и CFD подобны треугольнику ABC, поскольку углы при вершинах B и D являются соответственными. Из этого следует, что соотношение длин сторон треугольников AEB и CFD равно соотношению их высот, опущенных на сторону BC:
AE / CF = AB / CD
14 / 9 = AB / 8
AB = 112 / 9 см
Теперь мы знаем длины всех сторон треугольника ABC:
AB = 112 / 9 см, AC = 17 см, BC = 2AM = 17 см.
Полупериметр треугольника:
p = (AB + AC + BC) / 2 = (112/9 + 17 + 17) / 2 = 89/3 см.
Площадь треугольника:
S = квадратный корень (p(p-a)(p-b)(p-c)) = квадратный корень(89/3 * (89/3 - 112/9) * (89/3 - 17) * (89/3 - 17)) ≈ 84,7 (кв. см).
Ответ: S(ABC) ≈ 84,7 кв. см.
-
Автор:
robertuimw - 2 года назад
-
6
-
-
Добавить свой ответ
-
(Дам 100 баллов срочно!)До яких окенанів належать перелічені географічні об"єкти1.Охотське море2.о. Нова Земля3. Аденська затока4.Північне море5.Біскайська затока6.Малакський півострів7.Беренгова протока8.Півострів Корея9.Півострів Таймир10 о. Сицилія
-
Предмет:
География -
Автор:
alexzander - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
ПОМОГИТЕ СРОЧНО НУЖНО ДАМ 100 БАЛЛОВ
-
Предмет:
Информатика -
Автор:
woodward - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Выберите одну из тем и напишите эссе объемом 200 слов. 1. «Как убедить общественность Казахстана в необходимости рационального использования водныx ресурсов?». 2. «диета: за или против». Даю 50 баллов
-
Предмет:
Русский язык -
Автор:
natalybowen - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
2 Розв'яжи задачу. срочно нужна ваша допомога Із двох населених пунктів назустріч один одному виїхали 2 автомобілі. Швидкість першого автомобіля становить 100 км/год, що на 25 км/год більше за швидкість другого автомобіля. Яка відстань між на- селеними пунктами, якщо автомобілі зустрілися через 2 год після початку руху?
-
Предмет:
Математика -
Автор:
augustmcguire - 2 года назад
-
Ответов:
1 -
Смотреть
-
