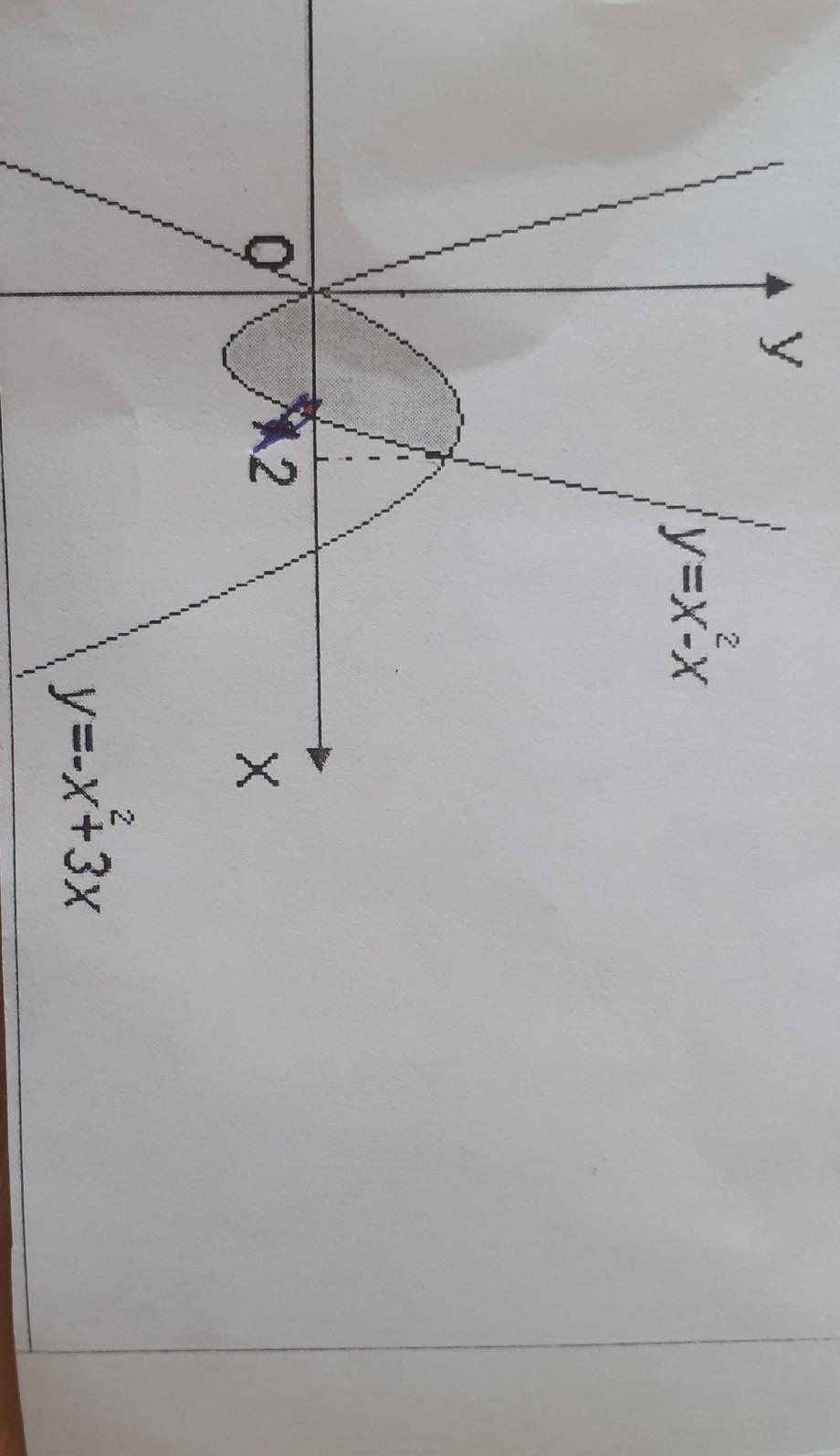
4. Найдите площадь фигуры, ограниченной линиями У 2 y=x-x при X y=-x+3x​

Для нахождения площади фигуры необходимо определить ее границы и интегрировать функцию, которая описывает ее форму.Границы фигуры определяются пересечением линий:y = x - x = 0y = -x + 3x = 2xОтсюда получаем, что границы фигуры находятся в точках (0,0) и (2,4).Функция, описывающая форму фигуры, зависит от координаты x и может быть найдена как разность y-координат двух прямых:f(x) = (-x + 3x) - (x - x) = 2xТаким образом, чтобы найти площадь фигуры, необходимо интегрировать функцию f(x) от x = 0 до x = 2:S = ∫[0,2] 2x dx = [x^2]0^2 = 4Ответ: площадь фигуры, ограниченной линиями y = x - x и y = -x + 3x, равна 4.