-
4. Сколько натуральных чисел N, 1 ≤ N ≤ 100, обладают свойством, что количество натуральных чисел n ≤ N где НОД(n, N) = 1 является делителем числа N?
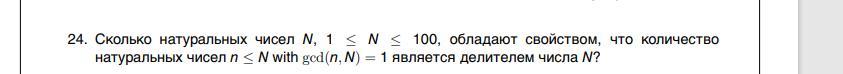
-
Предмет:
Математика -
Автор:
natalybowen - 2 года назад
-
Ответы 1
-
Ответ:
существует ровно 3 числа, удовлетворяющих условию
Пошаговое объяснение:
Предварительно заметим, что если
n=pv11pv22...pvss — разложение числа n на простые множители, то количество делителей числа n определяется по формуле
d(n)=(v1+1)(v2+1)...(vs+1).
Действительно, любой делитель d числа n имеет вид:
d=pα11pα22...pαss, где 0≤αi≤vi.
Показатель α1 можно выбрать v1+1 способами, показатель α2 можно выбрать v2+1 способами, и так далее, показатель αs можно выбрать vs+1 способами. Таким образом, количество способов выбрать показатели α1… αs или, что то же самое, выбрать делитель d числа n, которое равно (v1+1)(v2+1)...(vs+1).
1. Пусть n раскладывается на простые следующим образом:
n=3α5βpα11...pαss,
тогда количество делителей n равно
d(n)=(α+1)(β+1)(α1+1)...(αs+1).
2. Разложим исходное число на простые множители:
15=3⋅5.
После умножения n на 15 получим:
15n=3α+15β+1pα11...pαss,
d(15n)=(α+2)(β+2)(α1+1)...(αs+1).
3. Если количество делителей числа 15n увеличилось в 2 раза, то
d(15n)=2d(n) и (α+2)(β+2)(α1+1)...(αs+1)=2(α+1)(β+1)(α1+1)...(αs+1).
Отсюда находим
(α+2)(β+2)=2(α+1)(β+1),
αβ=2.
Таким образом, α=1, β=2 либо α=2, β=1.
Значит, для того чтобы после умножения на 15 количество делителей увеличилось в 2 раза, число должно иметь вид
3152q=75q или 3251p=45p,
где q, p взаимно просты с 15. Отметим, что числа этих видов не пересекаются, так как делятся на разную степень 3.
4. Посчитаем количество чисел указанных видов, не превосходящих 100.
Имеем
75q≤100,
q=1.
Получаем 1 число вида 75q.
Аналогично
45p≤100,
p≤2.
Числа p=1;2 подходят. Получаем 2 варианта чисел вида 45p.
-
Автор:
gertrudisduncan - 2 года назад
-
3
-
-
Добавить свой ответ
- Физика 10 клас
- Помогите пожалуйста!! и объясните как решается!!
-
a ) Look at the prompts . Write questions using the Present Perfect Continuous Tense . 1. Where / Mary / run / two hours ? ( At the stadium ) 2. How long / Ann / train in the gym ? ( For three hours ) 3. What game / Steve / play ? ( Basketball ) 4. Who / train / Sue / five years ? ( Mrs Fletcher )
-
Предмет:
Английский язык -
Автор:
beltrán93 - 2 года назад
-
Ответов:
1 -
Смотреть
-
- (30 балів) Схарактеризуйте трьома реченнями історичних діячів відповідно до їхньої ролі в подіях добн «застою»: Л. Брежнєв, П. Шелест, В. Щербицький (срочно )
