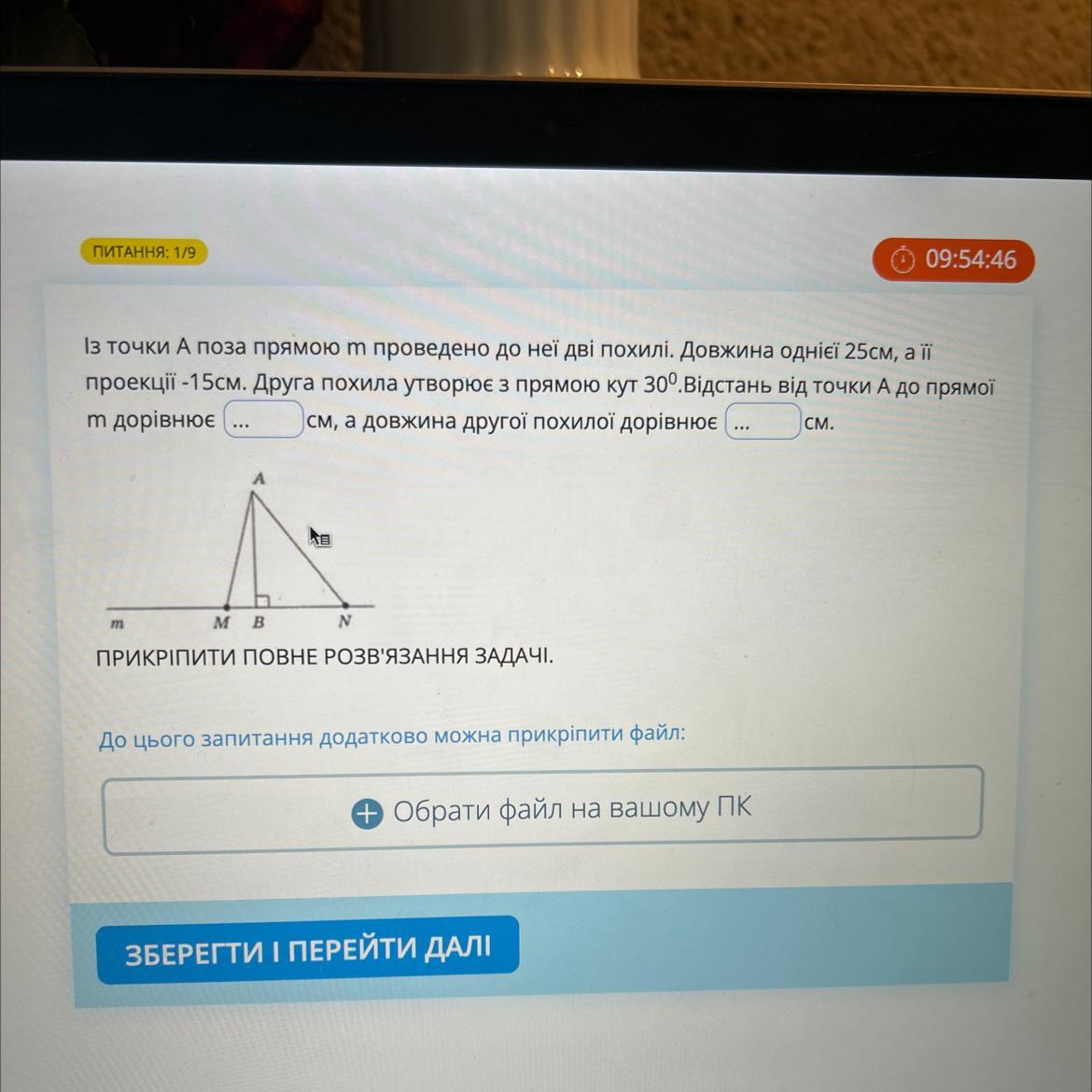
Із точки А поза прямою м проведено до неї дві похилі. Довжина однієï 25см, а її проекції-15см. Друга похила утворює з прямою кут 30°. Відстань від точки А до прямої m дорівнює см, а довжина другої похилоï дорівнює CM. m *** М В ПРИКРІПИТИ ПОВНЕ РОЗВ'ЯЗАННЯ ЗАДАЧІ. *** допоможіть, будь ласка

Ответ:

Отже, відстань дорівнює 7.5 см.

Пошаговое объяснение:

Задача вирішується за допомогою геометричних конструкцій та теореми Піфагора. Для початку позначимо точки: точку перетину похилої з прямою м позначимо як В, а точки проекції перпендикулярів на пряму м позначимо як С та D, як зображено на малюнку.

Так як точка С лежить на прямій м, відрізок АС є перпендикуляром до м. За властивостями прямокутного трикутника АСВ маємо:

AB = AC + BC

AB = 15 + 25 = 40 см

Також, з рівняння прямокутного трикутника ABD:

AD^2 = AB^2 - BD^2

BD = AB * sin(30°) = 20 см

AD = sqrt(AB^2 - BD^2) = sqrt(1400) см

Довжина другої похилої дорівнює BD + CD. Так як кут між м і CD дорівнює 90°, то CD = AD, тому:

BD + CD = BD + AD = 20 + sqrt(1400) см

Відстань від точки А до прямої м можна знайти як висоту прямокутного трикутника АСВ:

AM = AC * sin(30°) = 15/2 см

Таким чином, ми знайшли, що відстань від точки А до прямої м дорівнює 7.5 см, а довжина другої похилої дорівнює 20 + sqrt(1400) см.