-
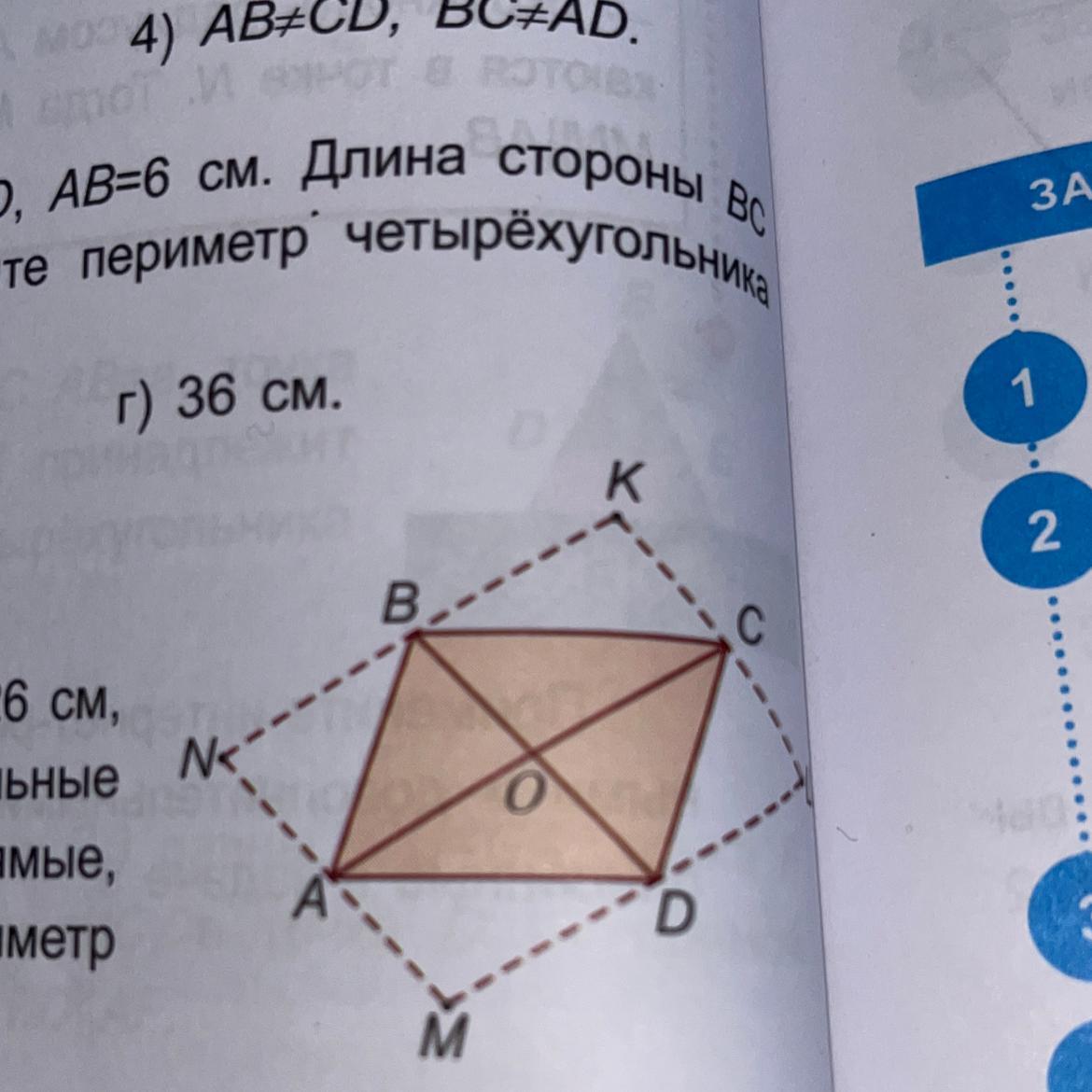
В' параллелограмме ABCD AC=32 см, BD=26 см, через точки А и С проведены прямые, параллельные диагонали BD, а через точки в и D - прямые, параллельные диагонали АС. Найдите периметр полученного четырёхугольника MNKL. Помогите пожалуйста!
-
Предмет:
Математика -
Автор:
sexton - 2 года назад
-
Ответы 1
-
Ответ:
В параллелограмме BD = AC = 32 см, значит, его высота h равна:
h = √(BD² - (AC/2)²) = √(26² - (32/2)²) = 24 см
Теперь рассмотрим четыре треугольника: AMN, NKL, KLC и CMD. Все они равнобедренные, так как две их стороны параллельны, а третья (высота) одинакова для всех.
Для каждого из этих треугольников высота равна h, а основание равно половине соответствующей стороны параллелограмма. Например, для треугольника AMN основание равно AN = AC/2 = 16 см. Таким образом, площадь каждого треугольника равна:
S = (1/2) × h × основание = (1/2) × 24 × (AC/2) = 192 кв. см
Теперь найдем периметр четырехугольника MNKL, который состоит из этих четырех равнобедренных треугольников. Для этого нужно сложить длины его сторон. Длины двух сторон мы уже знаем: MN = KL = AC = 32 см. Остальные две стороны находим с помощью теоремы Пифагора, примененной к треугольникам AMN и KLC:
MA² = AN² + NM² = 16² + h²
LC² = KL² - KC² = 32² - (AC/2)² = 32² - 16² = 960
Теперь длина каждой из оставшихся двух сторон равна сумме длин MA и LC, разделенной на 2:
MK = NL = (MA + LC)/2 = (√(16² + h²) + √960)/2
Итого, периметр четырехугольника MNKL равен:
P = 2×(MN + KL) + 2×(MK + NL) = 2×32 + 2×(√(16² + h²) + √960)/2 ≈ 113,1 см
Ответ: периметр четырехугольника MNKL равен около 113,1 см.
-
Автор:
valentinor96m - 2 года назад
-
2
-
-
Добавить свой ответ
- Знайдіть силу взаємодії між зарядами 4 нКл і 3 нКл, якщо відстань між ними 4 см.
- 5. Знайди суму коренів рівняння 9 - 1/16х² = 0 .
-
3. Переписати речення, підкреслити всі члени
речення.
а)Веселе сонечко ховалося у весняних хмарах.
б)За лісом широкі поля поволі спускалися
вниз.
в)Усе буйніше
розквітала прекрасна весна.
г)Надворі наші хлопці грали у футбол з друзями з сусіднього двору.
-
Предмет:
Українська мова -
Автор:
braveheart37 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
3) Из 300 учеников V классов школы в различных кружках занимается 138. Сколько процентов учащихся V классов занимается в кружках?
-
Предмет:
Математика -
Автор:
madalynnhorn - 2 года назад
-
Ответов:
1 -
Смотреть
-
