-
Найдите наименьшее целое решение неравенства: 7^{log_{1/5} } + x^{log_{1/5}7} \ll 2 * x^{log_{x}7 } (Нормальный знак "меньше" написать не получилось)
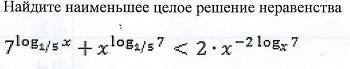
-
Предмет:
Математика -
Автор:
burns - 2 года назад
-
Ответы 1
-
Ответ:
Для решения неравенства можно воспользоваться методом замены переменной. Положим y = x log₇ 2, тогда неравенство примет вид:
7^(1/5 + log₇ y) < 2 * 7^(log₇ y)
Перепишем это неравенство в более удобной форме, выделив слагаемые с логарифмами:
7^(1/5) * 7^(log₇ y) < 2 * y * 7^(log₇ y)
Заметим, что 7^(log₇ y) = y, поэтому можно сократить на 7^(log₇ y) с обеих сторон:
7^(1/5) * y < 2 * y
Так как y > 0, то можно сократить на y:
7^(1/5) < 2
Таким образом, минимальное целое решение неравенства x будет равно:
x = ⌈log₇ 2⌉ = 1
Ответ: 1.
если помог отметь как лучший ответ
-
Автор:
francescaxdye - 2 года назад
-
8
-
-
Добавить свой ответ
Еще вопросы
- Укажите массу сульфатной кислоты, образующейся в результате взаимодействия 0.5 моль сульфур (VI) оксида с достаточным количеством воды.
- 1. Из предложенного списка выберите природные ресурсы: (4 балла) a) энергия приливов и отливов. б) школы. в) Чимбулак, г) минеральные, д) дороги, e) водные.
-
Помогите пожалуйста с немецким...
-
Предмет:
География -
Автор:
honey locks - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Все говорят Россия
-
Предмет:
Литература -
Автор:
aguilar - 2 года назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
