-
через точку а1 середину высоты sa треугольной пирамиды sabc провели сечение плоскостью параллельной плоскости основания пирамиды. найди площадь сечения если площадь треугольника abc равна 38
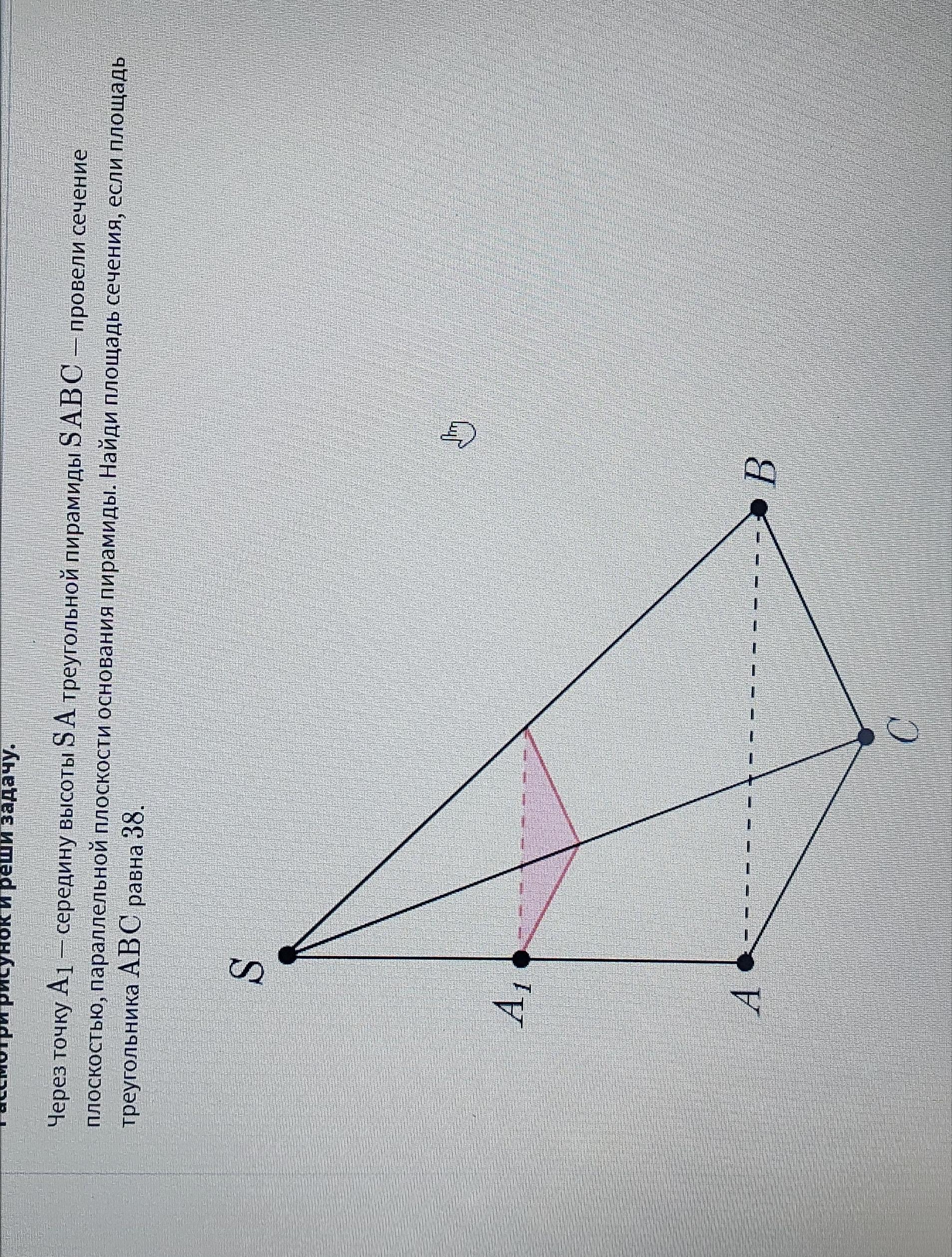
-
Предмет:
Математика -
Автор:
fionathornton - 2 года назад
-
Ответы 1
-
Для решения задачи нужно использовать свойства пирамиды и параллелограмма.Заметим, что сечение пирамиды плоскостью, параллельной основанию, образует параллелограмм. Обозначим точку пересечения высоты sa с плоскостью сечения через точку M.Так как точка A1 является серединой высоты sa, то AM является медианой треугольника SBC. Значит, AM делит BC пополам. Обозначим точку пересечения AM с BC через точку N.Так как AM || BC, то треугольники A1MN и A1BC подобны с коэффициентом 1:2, так как A1M является медианой треугольника A1BC и делит его на две равные части.Таким образом, длина отрезка MN равна BC/2. Заметим также, что треугольники ABC и AMN подобны с коэффициентом 1:2, так как углы при вершине A равны, а отрезок AM делит сторону BC пополам.Площадь треугольника ABC равна 38, значит, его высота sa равнаsa = 2 * S / BC = 2 * 38 / BC = 76 / BCТеперь можем найти длину отрезка MN:MN = BC / 2Используя теорему Пифагора в прямоугольном треугольнике A1MN, найдем длину отрезка AN:AN^2 = A1M^2 + MN^2AN^2 = (sa/2)^2 + (BC/2)^2AN^2 = (76/BC)^2 / 4 + BC^2 / 4AN^2 = 5776 / BC^2 + BC^2 / 4Чтобы найти площадь параллелограмма, нужно умножить длину стороны на высоту, проведенную к этой стороне. Высота, проведенная к стороне BC, проходит через точку A1 и параллельна плоскости основания. Таким образом, высота параллелограмма равна высоте пирамиды, то есть sa.Теперь можно найти площадь параллелограмма:S = AN * BCS = sqrt(5776 / BC^2 + BC^2 / 4) * BCS = BC * sqrt(5776 / BC^2 + 1/4)S = BC/2 * sqrt(23105 / BC^2 + 1)Ответ: площадь сечения пирамиды равна S = BC/2 * sqrt(231
-
Автор:
coreenvatf - 2 года назад
-
1
-
-
Добавить свой ответ
Еще вопросы
-
Находчивость Шерлока Холмса Конан Дойла
-
Предмет:
Литература -
Автор:
nathalyrosario - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Зробити спеціальні питання в пасивному стані
Ми прочитали багато книжок.
Мій сусід купив свою першу автівку два роки тому.
Мої браття часто читають американські статті після обіду.
Французький режисер зняв цей цікавий фільм у 1968 році.
Бабуся приготувала суп та спекла пиріг у першій половині дня.
Нещодавно я купив декілька кілограмів бананів та апельсинів на день народження доньки мого друга.
У лісі, діти побачили лося, що прибіг з іншої області.
Наша шкільна вчителька дала нам купу домашнього завдання на вихідні.
-
Предмет:
Английский язык -
Автор:
christina22 - 2 года назад
-
Ответов:
2 -
Смотреть
-
- Помогите с заданием по экономике
-
В выделенном предложении найдите слово ,в котором не совпадает количество букв и звуков.Обьясните причину
-
Предмет:
Русский язык -
Автор:
beltran - 2 года назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
