551.° Через центр О кола, описаного навколо трикутни- ка ABC, проведено пряму, яка перпендикулярна до сторони АС і перетинає сторону AB у точці М. Доведіть, що АМ =МС

Оскільки пряма, що проходить через центр описаного кола, перпендикулярна до сторони АС, то вона є середньою лінією трикутника ABC, яка ділить сторону AB навпіл. Отже, точка М є серединою сторони AB.При цьому, оскільки трикутник ABC описаний навколо кола, то сторона АВ є діаметром цього кола. Отже, кут АОВ дорівнює 90 градусів.За теоремою про кут у напівколі, кут, опромінений діаметром, дорівнює 90 градусів. Тому кут АМО дорівнює 90 градусів.З того, що кут АМО дорівнює 90 градусів, випливає, що точки А, М і О лежать на одному колі.Отже, ОМ – середня лінія трикутника АСМ і ділить сторону АС навпіл. Отже, АМ=МС.

Відповідь:

Дано:

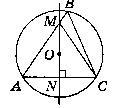
Коло з центром О описане навколо трикутника ABC. О є l, l ┴ АС, l ∩ АВ = М.

Довести: AM = МС.

Доведення:

Центр кола, описаного навколо трикутника, знаходиться в точці перетину

серединних перпендикулярів.

Якщо через центр кола проведена пряма l, яка перпендикулярна сторонi АС,

тоді N - точка перетину прямої l i сторони АС, буде серединою сторони AC

i тоді MN - медіана.

Якщо MN - висота i медіана, тоді ∆АМС - рівнобедрений, AM = МС.