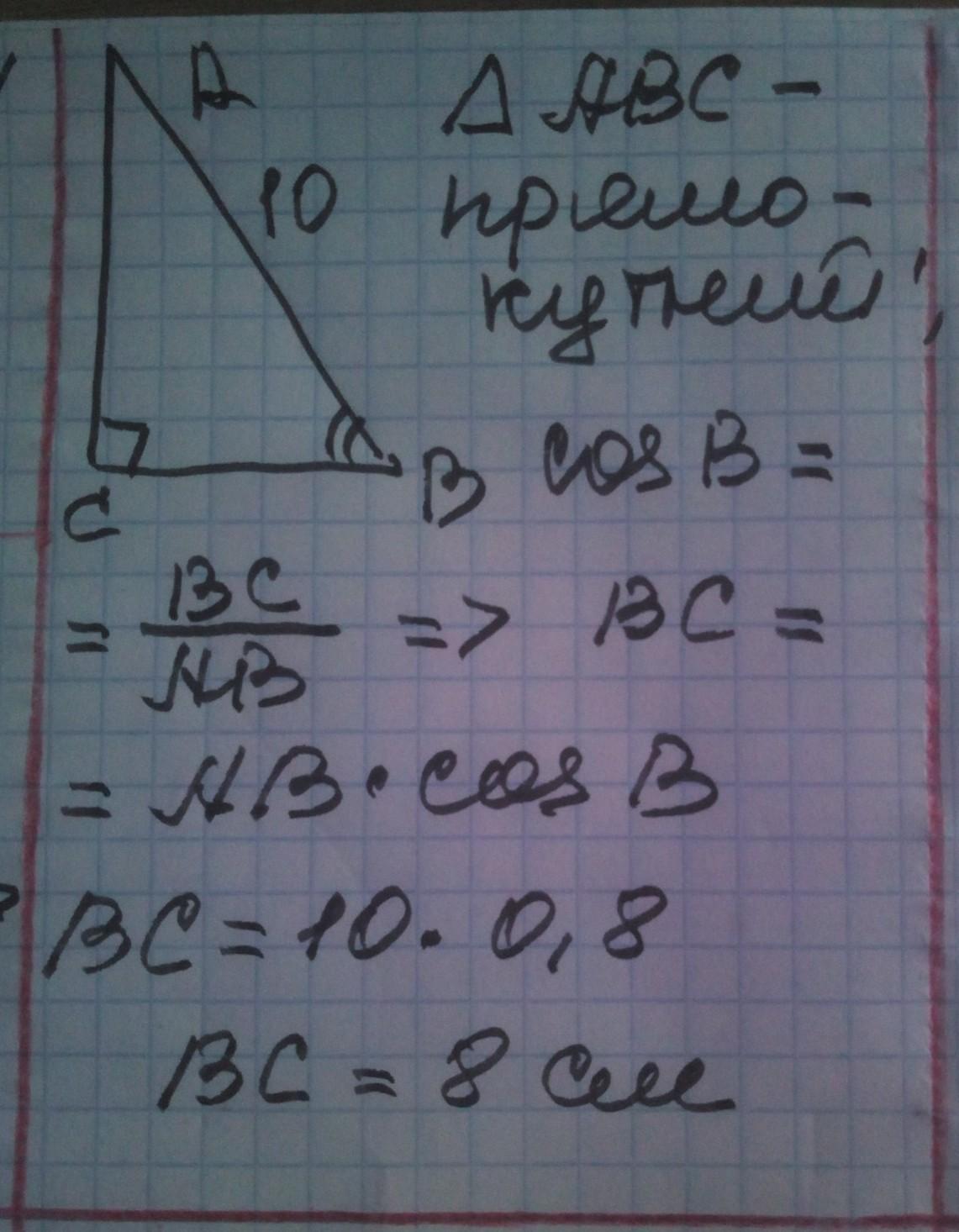
У трикутнику АВС ∟С=90°. Знайдіть ВС, якщо АВ=10 см і cos⁡В=0,8.

Відповідь: на фото бо я те саме тільки що робив

да

Пошаговое объяснение:

Застосуємо теорему Піфагора для трикутника ABC:

AC² = AB² + BC²

Оскільки ∟C = 90°, то sin⁡C = 1 і за теоремою синусів:

sin⁡B = BC/AC

Тоді:

BC = AC*sin⁡B

Також за умовою задачі cos⁡B = 0,8, звідки sin⁡B = sqrt(1 - cos²B) = sqrt(1 - 0,8²) = 0,6

Залишається знайти довжину AC:

AC = sqrt(AB² + BC²) = sqrt(10² + (AC*sin⁡B)²)

Або, підставивши значення sin⁡B:

AC = sqrt(10² + (AC*0,6)²)

Розв'язуємо рівняння відносно AC:

AC² = 10² + (AC*0,6)²

AC² = 100 + 0,36AC²

0,64AC² = 100

AC² = 156,25

AC = sqrt(156,25) = 12,5

Отже, довжина ВС дорівнює 12,5 см.