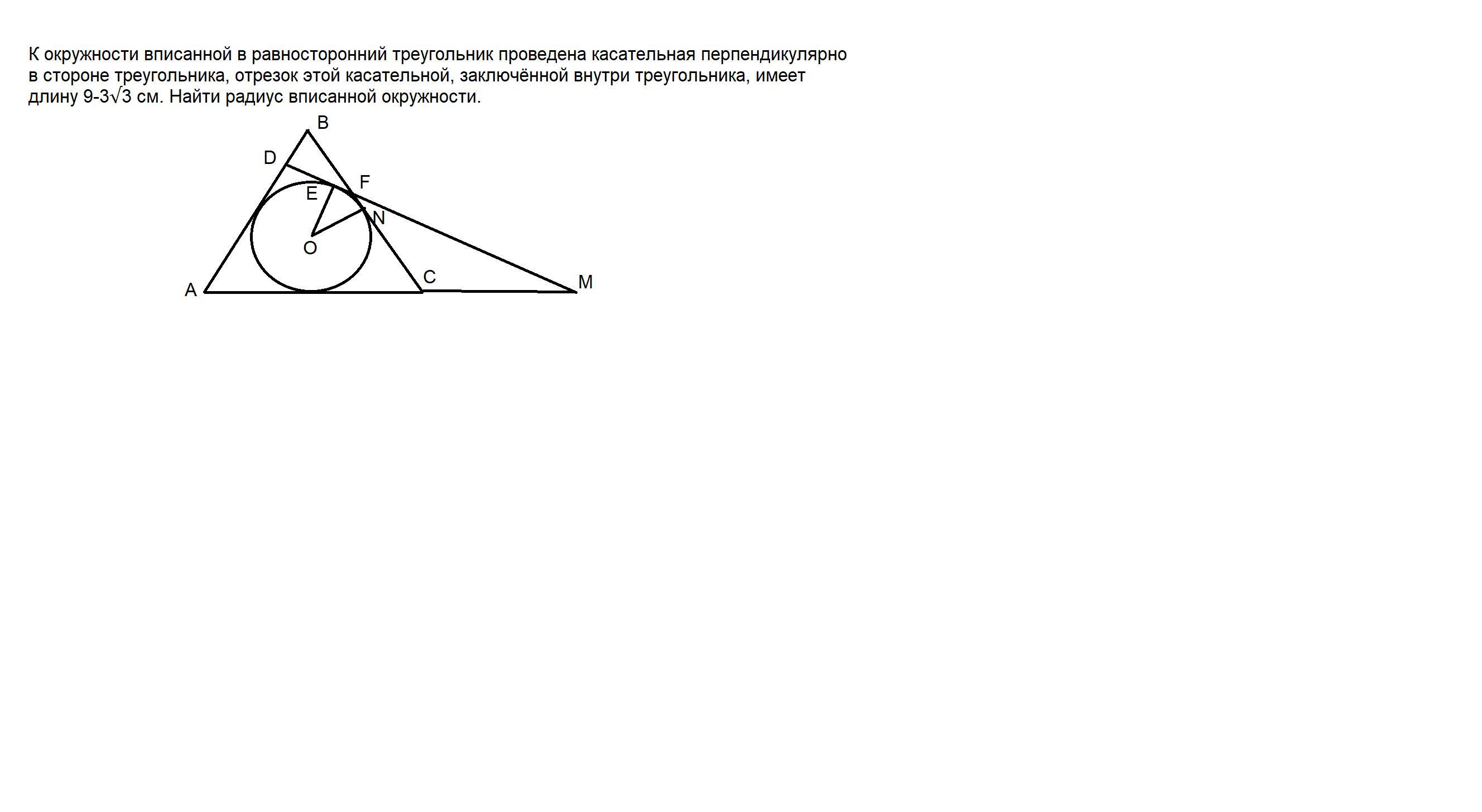
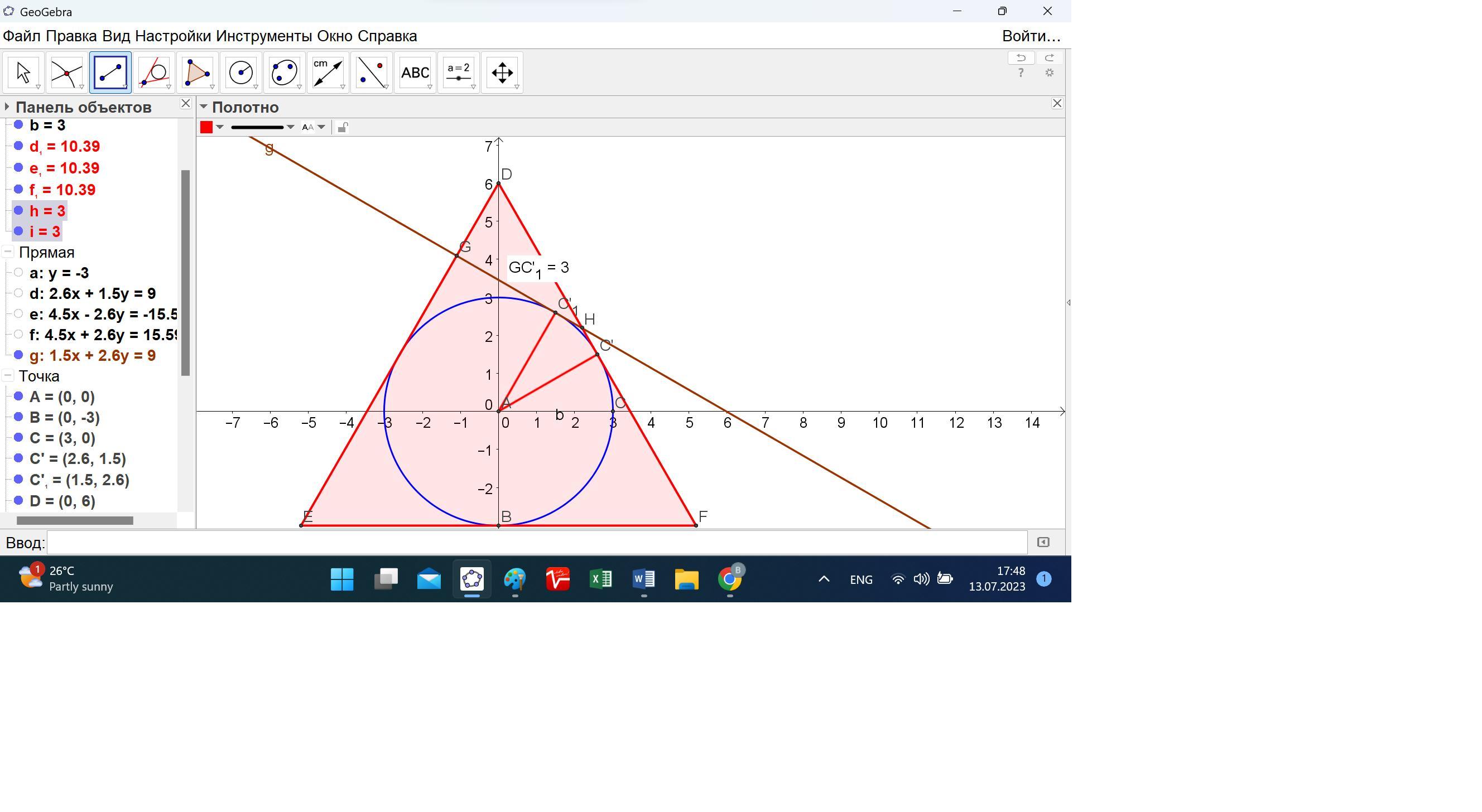
К окружности вписанной в равносторонний треугольник проведена касательная перпендикулярно в стороне треугольника, отрезок этой касательной, заключённой внутри треугольника, имеет длину 9-3√3 см. Найти радиус вписанной окружности.

Ответ: 3 см.

Пошаговое объяснение:

Угол EON как взаимно перпендикулярный к касательным DM и BC равен 30 градусов.

ЕF = Rtg(30°/2) = R (1 – (√3/2))/(1/2) = 2R(1 – (√3/2)).

DE = R.

По заданию DF = 9 - 3√3.

Так как DF = DE + ЕF = R + 2R(1 – (√3/2)).

9 - 3√3 = = R + 2R(1 – (√3/2)).

Отсюда R = (9 - 3√3)/(1 + 2(1 – (√3/2)) = (9 - 3√3)/(1 + 2 – √3) = 3(3 - √3)/(3 - √3) = 3.