-
Допоможіть будь ласка!!!!Потрібно знайти: 1. (2p+3q)*(x-2r) 2. (p-2r)x(q + 3x) 3. Орт вектора e=p+r-х 4. cos(p+q, r-x) 5. пp (q+2p) 6. (pq)r 7. Довжини діагоналей паралелограма, побудованого на векторах p і q 8. Площу паралелограма, побудованого на векторах r і х 9. (p*x)*r, чи будуть вектори р,q, r компланарними? Яку трійку вони утворюють? 10. Чому дорівнює об'єм паралелепіпеда, побудованого на векторах p, q, r? 11. Чи утворюють вектори p, q, r базис? Якщо утворюють, то знайти розклад вектора х по цьому базису.
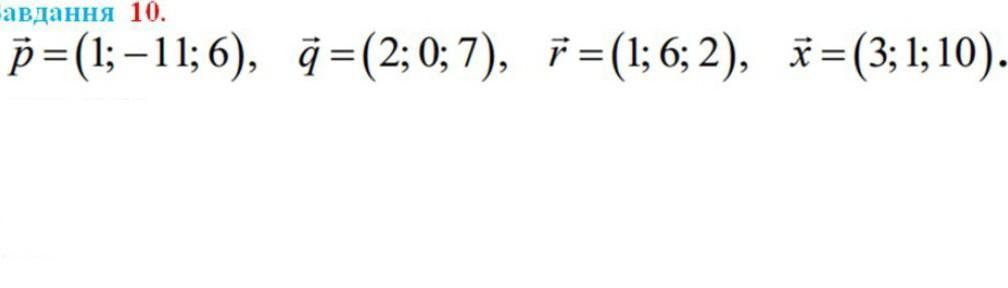
-
Предмет:
Математика -
Автор:
jase - 2 года назад
-
Ответы 1
-
1. (2п+3д)*(х-2р) = 2пкс - 4пр + 3дх - 6кр2. (p-2r)x(q + 3x) = pqx + 3px^2 - 2rqx - 6rx^23. Орт-вектор e = p + r - x4. cos(p+q, r-x) = cos(p+q)*cos(r-x) + sin(p+q)*sin(r-x)5. х(q+2p) = xq + 2xp6. (пк)р = р^2к7. Длины диагоналей параллелограмма, построенного на векторах p и q: ||p+q|| и ||p-q||8. Площадь параллелограмма, построенного на векторах p и q: ||p x q|| (величина векторного произведения p и q)9. (p*x)*r: Это выражение неясно. Пожалуйста, предоставьте больше информации.10. Объем параллелепипеда, построенного на векторах p, q и r: |(p x q) · r| (абсолютное значение скалярного произведения векторного произведения p и q на r)11. Чтобы определить, образуют ли векторы p, q, r базис, необходима дополнительная информация. В частности, размерность векторного пространства, которому они принадлежат.
-
Автор:
jamya1no1 - 2 года назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
МНОГО БАЛОВ
1 На підставі чого Гофмана називають «універсальною людиною в мистецтві»?
2 Які зміні відбуваються утворі з крихіткою Цахесом? (за твором Гофмана «Крихітка Цахес на прізвисько Цинобер»).
-
Предмет:
Литература -
Автор:
felipeunderwood - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Надо перевести координаты точек в десятичную систему счисления. И построить рисунок на координатной плоскости.
-
Предмет:
Информатика -
Автор:
lola76 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Пожалуйстаа,срочноо,нужно сдать сегодня.5 речень на тему:Чому я себе відношу до адекватної самооцінки.Чому я так вважаю,треба пояснити.
-
Предмет:
Другие предметы -
Автор:
trevino - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Срочноо,пожалуйста.Напишіть есе-роздум на тему"Чи перебуває Україна в замкненому колі бідності?"
-
Предмет:
Другие предметы -
Автор:
jadencobb - 2 года назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
