-
Определённый интеграл. Помогите пожалуйста, уже 3 часа пытаюсь это решить, не выходит
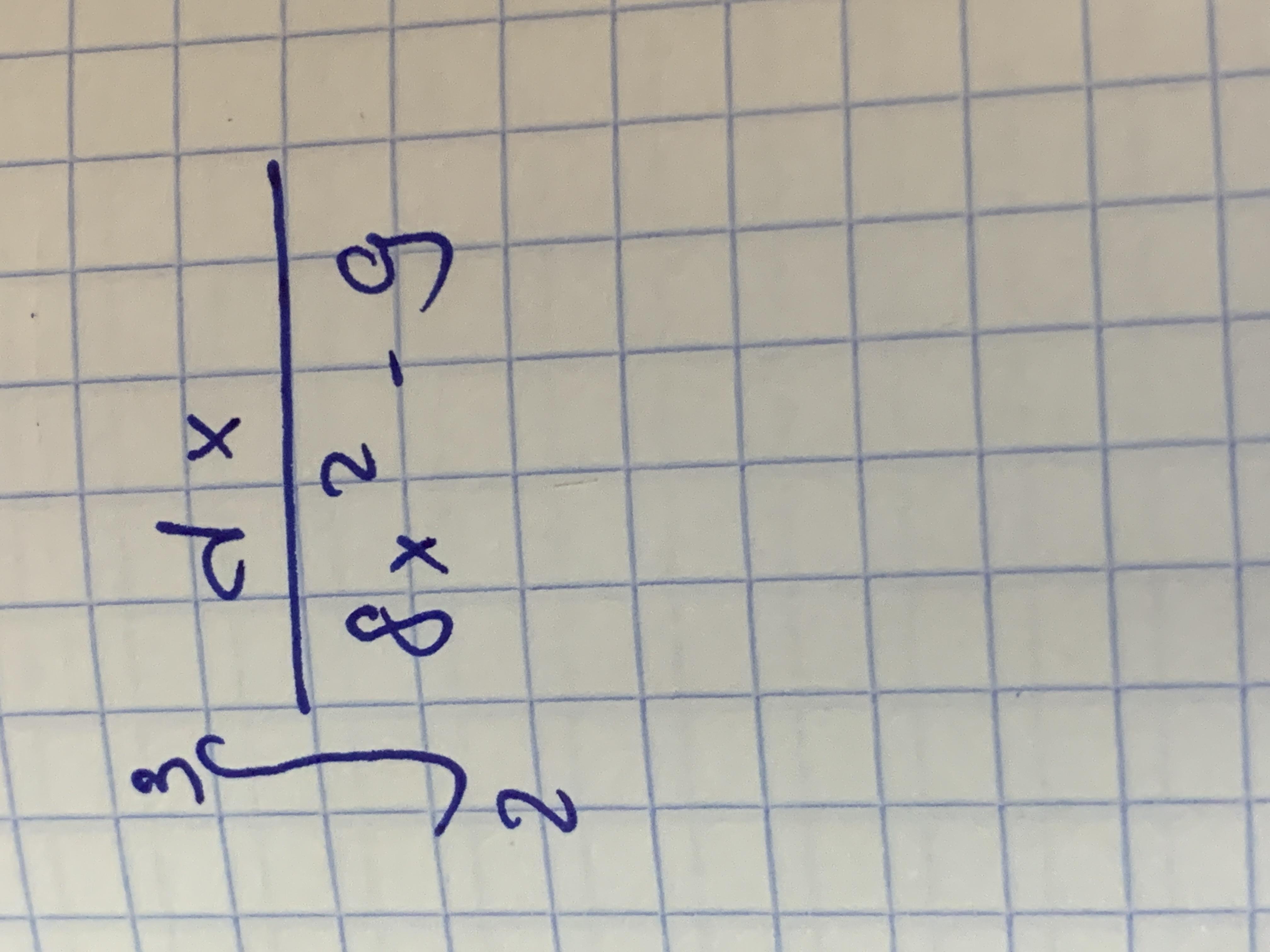
-
Предмет:
Математика -
Автор:
shawn - 2 года назад
-
Ответы 1
-
$I=\int \frac{dx}{8x^2-9}=-\frac{1}{9}\int \frac{dx}{1-8x^2/9}\overset{2\sqrt{2}x/3=t}{=}-\frac{1}{6\sqrt{2}}\int \frac{dt}{1-t^2}=-\frac{1}{6\sqrt{2}}\mathrm{ath} \; t+C$$I=-\frac{1}{6\sqrt{2}}\mathrm{ath}\frac{2\sqrt{2}x}{3}+C\Rightarrow J=\int\limits_{2}^{3}\frac{dx}{8x^2-9}=-\frac{1}{6\sqrt{2}}\mathrm{ath}\frac{2\sqrt{2}\cdot 3}{3}+\frac{1}{6\sqrt{2}}\mathrm{ath}\frac{2\sqrt{2}\cdot 2}{3}$$J=-\frac{1}{6\sqrt{2}}\left (\mathrm{ath}2\sqrt{2}-\mathrm{ath}\frac{4\sqrt{2}}{3} \right )=-\frac{1}{6\sqrt{2}}\left ( -\mathrm{ath}\frac{2\sqrt{2}}{13} \right )=\frac{1}{6\sqrt{2}}\mathrm{ath}\frac{2\sqrt{2}}{13}$
-
Автор:
xavier355 - 2 года назад
-
1
-
-
Добавить свой ответ
-
Світ добра та людяності Ульфа Старка Чи вмієш ти свистати Йогонно
-
Предмет:
Українська література -
Автор:
skinner - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
почему Алидарку нельзя назвать романтичным героем?
-
Предмет:
Беларуская мова -
Автор:
mister17 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
как сдержать улыбку когда смотришь на человека?
-
Предмет:
Другие предметы -
Автор:
isabellajohnson - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Контрольная по русскому! помогите пожалуйста
-
Предмет:
Русский язык -
Автор:
samanthaproctor - 2 года назад
-
Ответов:
2 -
Смотреть
-
